Giúp nốt mình mấy câu này với
H24
Những câu hỏi liên quan
 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
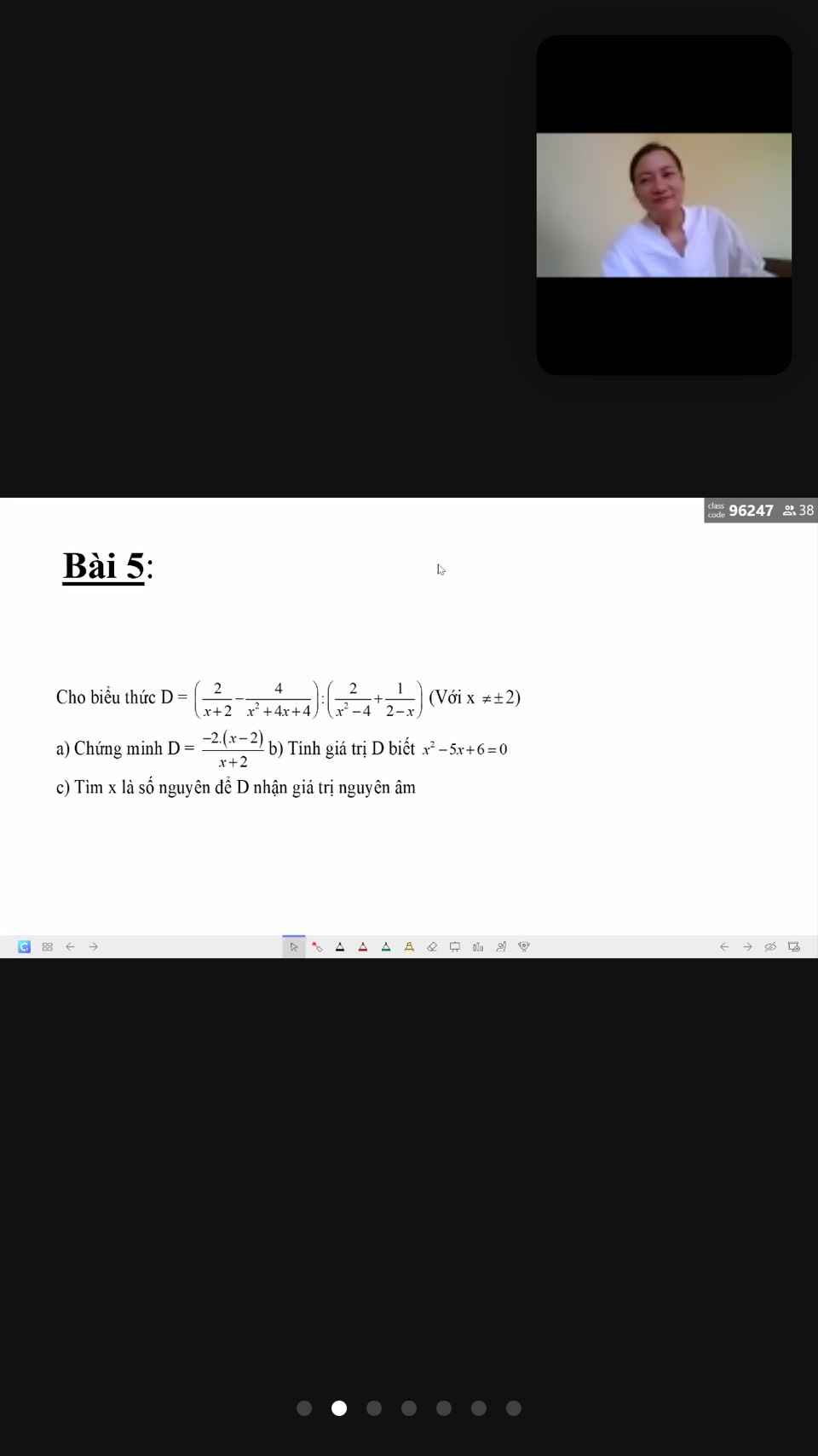
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
Đúng 3
Bình luận (2)
D nguyên âm \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\left(x-2\right)< 0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}-2\left(x-2\right)>0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>2\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\x< -2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x>2\\x< -2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a:Ta có: \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}\cdot\dfrac{\left(x+2\right)\left(x-2\right)}{-x}\)
\(=\dfrac{-\left(x-2\right)}{x+2}\)
b: Ta có: \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
hay x=3
Thay x=3 vào D, ta được:
\(D=\dfrac{-\left(3-2\right)}{3+2}=-\dfrac{1}{5}\)
Đúng 1
Bình luận (1)
Các bạn giải nốt giúp mình hai câu này với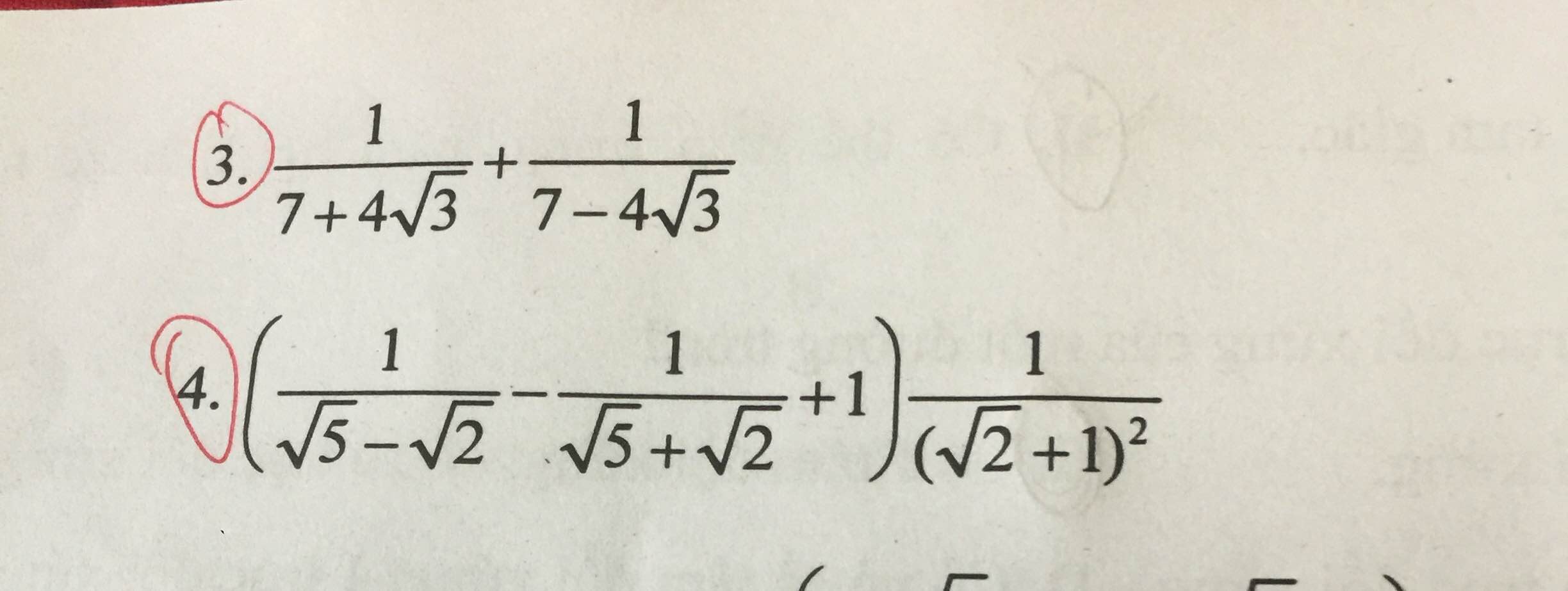
3: \(=7-4\sqrt{3}+7+4\sqrt{3}=14\)
4: \(=\left(\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\right)\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Giúp mình làm nốt mấy câu còn lại câu nào sai sủa giúp mình

giúp mình nốt câu này nhé các bạn
\(f'\left(x\right)=2x^2-x\)
\(f'\left(x\right)\ge0\Leftrightarrow2x^2-x\ge0\)
\(\Leftrightarrow x\left(2x-1\right)\ge0\Rightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\le0\end{matrix}\right.\)
Đúng 1
Bình luận (0)

giúp mình nốt câu này các bạn ơi
\(\left\{{}\begin{matrix}BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BD\perp SC\)
Mặt khác \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
b.
Từ A kẻ \(AH\perp SB\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp AH\)
\(\Rightarrow AH\) là đường vuông góc chung của AD và SB
\(\Rightarrow AH=d\left(SB;AD\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{2}{a^2}\Rightarrow AH=\dfrac{a\sqrt{2}}{2}\)
Gọi O là tâm đáy, từ O kẻ \(OK\perp SC\)
Mà \(BD\perp\left(SAC\right)\) theo câu a \(\Rightarrow BD\perp OK\)
\(\Rightarrow OK\) là đường vuông góc chung của SC và BD hay \(OK=d\left(SC;BD\right)\)
\(AC=AB\sqrt{2}=a\sqrt{2}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{3}\)
\(OK=OC.sin\widehat{SCA}=\dfrac{1}{2}AC.\dfrac{SA}{SC}=\dfrac{a\sqrt{6}}{6}\)
Đúng 0
Bình luận (0)
mong các bạn giúp mình giải nốt câu này. mình cần gấp
Đọc tiếp
mong các bạn giúp mình giải nốt câu này. mình cần gấp![]()
Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)
Đúng 2
Bình luận (1)
Giúp mình mấy câu này với ( đc thì viết giúp mình câu nào sai - đúng với)

58800kg=...........tạ giúp mình làm nốt 1 câu này nữa thôi nha!!!
TL:588 tạ nha
Xem thêm câu trả lời
giúp mình nốt bài này với
mình cảm ơn nhìu
Xem thêm câu trả lời








