Từ một điểm A ngoài (O;R) kẻ hai tiếp tuyến AB,AC với (O) (B,C là hai tiếp điểm). Đường thẳng qua B và song song với OC cắt đường thẳng qua C và song song với OB tại F. Chứng minh tứ giác BFCO là hình thoi
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
VP
Những câu hỏi liên quan
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Đọc tiếp
Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O Từ một điểm A nằm ngoài đường tròn tâm O vẽ tiếp tuyến AB ( B là tiếp điểm ) và cát tuyết ACD . Gọi I là trung điểm của CD . Vẽ dây cung BE vuông góc với OA tại H . Chứng minh AE là tiếp tuyến của đường tròn tâm O
Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD 2OH
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
dễ ẹc thì lm cho mk coi đi
mk ko bt lm
Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AOa) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.b) Cho AB 8cm;BC 9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE góc BDE.
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AO
a) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.
b) Cho AB = 8cm;BC =9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)
c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE = góc BDE.
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)
Đúng 0
Bình luận (0)
cho đương tròn (O,R)và một điểm A nằm ngoài đường tròn (O,R).Từ A vẽ hai điểm tiếp tuyến AB,AC của (O,R) ( B,C là tiếp điểm).Từ B vẽ đường kính BD của (O ,R), đường thẳng AD cắt (O,R) tại E (khác D) . CM 4 điểm A,B,C,O cùng thuộc 1 đường tròn
Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài (O) vẽ hai tiếp tuyến MA, MB (A,B là tiếp điểm) a) Chứng minh 4 điểm M,A,O,B cùng thuộc một đường tròn b) Vẽ I là trung điểm MB. Nối AI cắt (O) tại C. Chứng minh IB²=IC.IA c) MC cắt (O) tại D. Chứng minh MB²= MC.MD Suy ra MC.MD=IC.IA
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{IBC}\) là góc tạo bởi tiếp tuyến BI và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{IBC}=\widehat{BAC}\)
Xét ΔIBC và ΔIAB có
\(\widehat{IBC}=\widehat{IAB}\)
\(\widehat{BIC}\) chung
Do đó: ΔIBC~ΔIAB
=>\(\dfrac{IB}{IA}=\dfrac{IC}{IB}\)
=>\(IB^2=IA\cdot IC\)
c: Xét (O) có
\(\widehat{MBC}\) là góc tạo bởi tiếp tuyến BM và dây cung BC
\(\widehat{CDB}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MBC}=\widehat{CDB}\)
Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC~ΔMDB
=>\(\dfrac{MB}{MD}=\dfrac{MC}{MB}\)
=>\(MB^2=MD\cdot MC\)
Đúng 2
Bình luận (0)
a. Em tự giải
b.
Ta có: IB là tiếp tuyến (O) tại B nên \(\widehat{BAC}=\widehat{CBI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến - dây cung cùng chắn BC)
Xét hai tam giác ABI và BCI có:
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{CBI}\left(cmt\right)\\\widehat{BIA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta ABI\sim\Delta BCI\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IB}{IC}\Rightarrow IB^2=IC.IA\)
c.
Ta có \(\widehat{BDC}\) và \(\widehat{MBC}\) là góc nội tiếp và góc tạo bởi tiếp tuyến sây cung cùng chắn BC
\(\Rightarrow\widehat{BDC}=\widehat{MBC}\)
Xét hai tam giác MBD và MCB có:
\(\left\{{}\begin{matrix}\widehat{BMD}\text{ chung}\\\widehat{BDC}=\widehat{MBC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBD\sim\Delta MCB\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MC}=\dfrac{MD}{MB}\Rightarrow MB^2=MC.MD\)
Đẳng thức cuối em ghi sai.
Do I là trung điểm MB \(\Rightarrow MB=2IB\Rightarrow MB^2=4IB^2\)
\(\Rightarrow MC.MD=4IC.IA\) (đây mới là đẳng thức đúng)
Đúng 3
Bình luận (0)
Từ một điểm A ở ngoài đường tròn left(Oright), kẻ hai tiếp tuyến AB.AC với đường tròn tâm O (B,C là các tiếp điểm).
a) Chứng minh bốn điểm A,B,O,C cùng thuộc một đường tròn.
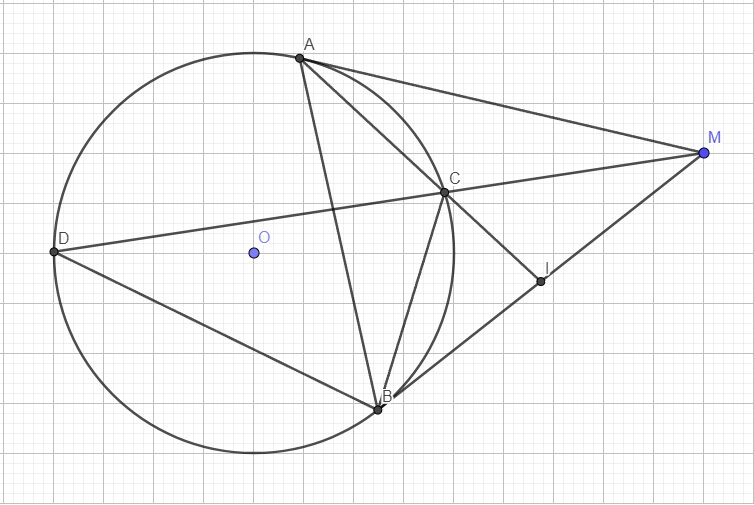
b) Vẽ cát tuyến ADE (D nằm giữa A,E) sao cho điểm O nằm trong góc EAB. Gọi I là trung điểm của ED. BC cắt OA,EA theo thứ tự tại H,K. Chứng minh: OAperp BC tại H và AHcdot AOAKcdot AI.
c) Tia AO cắt left(Oright) tại hai điểm M,N (M nằm giữa A,N). Gọi P là trung điểm HN, đường vuông góc với BP vẽ từ H cắt tia BM tại S. Chứng m...
Đọc tiếp
Từ một điểm \(A\) ở ngoài đường tròn \(\left(O\right)\), kẻ hai tiếp tuyến \(AB.AC\) với đường tròn tâm \(O\) (\(B,C\) là các tiếp điểm).
a) Chứng minh bốn điểm \(A,B,O,C\) cùng thuộc một đường tròn.
b) Vẽ cát tuyến \(ADE\) (\(D\) nằm giữa \(A,E\)) sao cho điểm \(O\) nằm trong góc \(EAB\). Gọi \(I\) là trung điểm của \(ED\). \(BC\) cắt \(OA,EA\) theo thứ tự tại \(H,K\). Chứng minh: \(OA\perp BC\) tại \(H\) và \(AH\cdot AO=AK\cdot AI\).
c) Tia AO cắt \(\left(O\right)\) tại hai điểm \(M,N\) (\(M\) nằm giữa \(A,N\)). Gọi \(P\) là trung điểm \(HN\), đường vuông góc với \(BP\) vẽ từ \(H\) cắt tia \(BM\) tại \(S\). Chứng minh \(MB=MS\).
a/
Ta có
\(\widehat{ABO}=\widehat{ACO}=90^o\) => B và C cùng nhìn AO dưới 1 góc \(90^o\)
=> B; C nằm trên đường tròn đường kính AO => A; B; O; C cùng nằm trên 1 đường tròn
b/
Xét tg vuông ABO và tg vuông ACO có
OA chung; OB=OC (bán kính (O)) => tg ABO = tg ACO (hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)
Xét tg ABH và tg ACH có
AH chung
AB=AC (2 tiếp tuyến cùng xp từ 1 điểm...)
tg ABO = tg ACO (cmt) \(\Rightarrow\widehat{BAO}=\widehat{CAO}\)
=> tg ABH = tg ACH (c.g.c) \(\Rightarrow\widehat{AHB}=\widehat{AHC}\) Mà \(\widehat{AHB}+\widehat{AHC}=\widehat{BHC}=180^o\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\Rightarrow OA\perp BC\) tại H
Ta có ID=IE (gt) \(\Rightarrow OI\perp DE\) (trong đường tròn đường thẳng đi qua tâm và trung điểm của dây cung thì vuông góc với dây cung)
Xét tg vuông AHK và tg vuông AIO có
\(\widehat{OAI}\) chung
=> tg AHK đồng dạng với tg AIO
\(\Rightarrow\dfrac{AH}{AI}=\dfrac{AK}{AO}\Rightarrow AH.AO=AK.AI\)
c/
Đúng 2
Bình luận (0)
Từ một điểm A ở ngoài đường tròn left(Oright), kẻ hai tiếp tuyến AB,AC với đường tròn tâm O (B,C là các tiếp điểm).a) Chứng minh bốn điểm A,B,O,C cùng thuộc một đường tròn.b) Vẽ cát tuyến ADE (D nằm giữa A,E) sao cho điểm O nằm trong góc EAB. Gọi I là trung điểm của ED. BC cắt OA,EA theo thứ tự tại H,K. Chứng minh OAperp BC tại H và AHcdot AOAKcdot AI.c) Tia AO cắt left(Oright) tại hai điểm M,N (M nằm giữa A,N). Gọi P là trung điểm của HN, đường vuông góc với BP vẽ từ H cắt tia BM tại S. Chứng m...
Đọc tiếp
Từ một điểm \(A\) ở ngoài đường tròn \(\left(O\right)\), kẻ hai tiếp tuyến \(AB,AC\) với đường tròn tâm \(O\) (\(B,C\) là các tiếp điểm).
a) Chứng minh bốn điểm \(A,B,O,C\) cùng thuộc một đường tròn.
b) Vẽ cát tuyến \(ADE\) (\(D\) nằm giữa \(A,E\)) sao cho điểm \(O\) nằm trong góc \(EAB\). Gọi \(I\) là trung điểm của \(ED\). \(BC\) cắt \(OA,EA\) theo thứ tự tại \(H,K\). Chứng minh \(OA\perp BC\) tại \(H\) và \(AH\cdot AO=AK\cdot AI\).
c) Tia \(AO\) cắt \(\left(O\right)\) tại hai điểm \(M,N\) (\(M\) nằm giữa \(A,N\)). Gọi \(P\) là trung điểm của \(HN\), đường vuông góc với \(BP\) vẽ từ \(H\) cắt tia \(BM\) tại \(S\). Chứng minh \(MB=MS\).
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=> A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
Ta có: ΔOED cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)ED tại I
=>OI\(\perp\)AE tại I
Xét ΔAIO vuông tại H và ΔAHK vuông tại H có
\(\widehat{IAO}\) chung
Do đó: ΔAIO~ΔAHK
=>\(\dfrac{AI}{AH}=\dfrac{AO}{AK}\)
=>\(AH\cdot AO=AI\cdot AK\)
Đúng 2
Bình luận (0)
Từ một điểm A nằm ngoài (O;R), kẻ tiếp tuyến AB và AC với (O) (B,C là tiếp điểm). Vẽ đường kính CD của (O). Chứng minh:
a. Chứng minh 4 điểm A,B,C,O cùng thuộc một đường tròn. Xác định tâm đường tròn đó.
b. Gọi E là giao điểm của AD và (O) (E khác D). H là giao điểm của OA và BC. Chứng minh AH.AO = AE.AD
từ điểm A ngoài đường tròn (O;R) vẽ hai tiếp tuyến Ab và AC (B,C là hai tiếp điểm)
a) Chứng minh A,B,O,C cùng thuộc một đường tròn
Vì AB là tiếp tuyến của ( O )
Nên \(AB\perp OB\Rightarrow\widehat{ABO}=90^o\)
Tương tự \(\widehat{ACO}=90^o\)
Xét tứ giác \(ABOC\)
\(\widehat{ABO}+\widehat{ACO}=90^o+90^o=180^o\)
Nên ABOC là tứ giác nội tiếp đường tròn
=> A,B,O,C cùng thuộc một đường tròn