vẽ đồ thị hàm số y=\(\dfrac{1}{3}x\)
(viết câu trả lời đầy đủ)
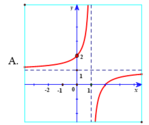
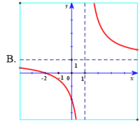
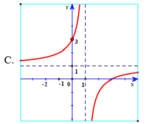
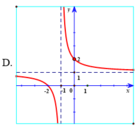
Hàm số y = x - 2 x - 1 có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
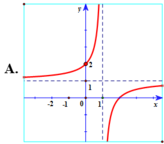
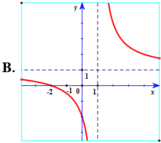
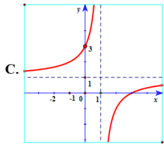
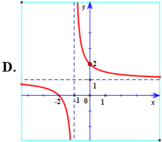
Chọn A.
[Phương pháp tự luận]
Hàm số y = x - 2 x - 1 có tiệm cận đứng x = 1 . Tiệm cận ngang y = 1 nên loại trường hợp D.
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm ( 0 ; 2 ) nên chọn đáp án A.
[Phương pháp trắc nghiệm]
d d x x - 2 x - 1 x = 10 = 1 81 > 0 suy ra hàm số y = x - 2 x - 1 đồng biến trên tập xác định, loại B, D.
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm ( 0 ; 2 ) nên chọn đáp án A.
Hàm số y = x - 2 x - 1 có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
Chọn A.
Hàm số y = x - 2 x - 1 có tiệm cận đứng x = 1.
Tiệm cận ngang y = 1 nên loại trường hợp D.
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm (0; 2) nên chọn đáp án A.
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
trong mặt phẳng tọa độ Oxy cho ĐỒ THỊ HÀM SỐ y=axlaf đường thẳng OM với M(-3;2).
Câu hỏi :
- Điểm N(x0;y0) (( 0 là số nhỏ nhé )) thuộc đồ thị hàm số trên. Tính \(\frac{x0-3}{y0+2}\)
{ Bạn nào có câu trả lời nhanh - đúng - đầy đủ nhất thì mình sẽ chon } ^-^
Hàm số y = 2 + 2 x 2 + x có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
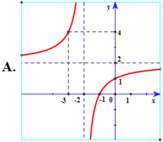
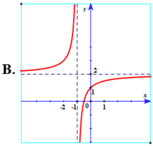
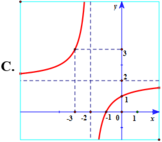
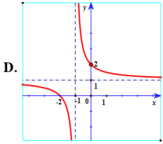
Chọn A.
[Phương pháp tự luận]
Hàm số y = 2 + 2 x 2 + x có tiệm cận đứng x = - 2 . Tiệm cận ngang y = 2 nên loại đáp án B, D.
Đồ thị hàm số y = 2 + 2 x 2 + x đi qua điểm - 3 ; 4 nên chọn đáp án A.
[Phương pháp trắc nghiệm]
d d x 2 + 2 x 2 + x x = 1 ≈ 0 , 2 > 0 suy ra hàm số y = 2 + 2 x 2 + x đồng biến trên tập xác định, loại D.
Sử dụng chức năng CALC của máy tính: C A L C → - 3 = 4 nên chọn đáp án A.
Hàm số y = 2 + 2 x 2 + x có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
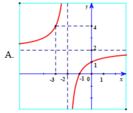
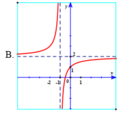
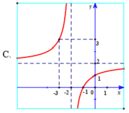
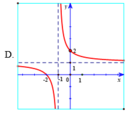
Chọn A.
Hàm số y = 2 + 2 x 2 + x có tiệm cận đứng x = -2.
Tiệm cận ngang y = 2 nên loại đáp án B, D.
Đồ thị hàm số y = 2 + 2 x 2 + x đi qua điểm (- 3; 4) nên chọn đáp án A.
Vẽ đồ thi hàm số y=2x
Hỏi M(1;-4) VÀ N(1/2;1) có thuộc đồ thị hàm số y=2x không?
Vẽ đồ thị và trả lời chi tiết
Điểm N thuộc đồ thị vì \(y_N=1=2\cdot x_N=2\cdot\dfrac{1}{2}\)
Điểm M ko thuộc đồ thị vì \(y_M=-4< >2\cdot x_M\)
Lời giải:
ĐTHS $y=2x$:
Muốn kiểm tra xem 1 điểm có thuộc đths không thì ta thay tung độ và hoành độ của đồ thị đó vào phương trình đồ thị đó xem có thỏa mãn không là được.
$x_M=1; y_M=-4$ nên $y_M\neq 2x_M$ nên $M$ không thuộc đths $y=2x$
$x_N=\frac{1}{2}; y_N=2$ nên $y_N=2x_N$ nên $N$ thuộc đths $y=2x$
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Đồ thị của hàm số y = ax2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Đồ thị hàm số y = ax2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Câu 2: Cho hàm số \(y=f\left(x\right)=\dfrac{1}{2}x^2\) có đồ thị là (P)
a) Tính f(-2)
b) Vẽ đồ thị (P) trên mặt phẳng với hệ trục tọa độ Oxy
c) Cho hàm số y = 2x + 6 (d). Tìm tọa độ giao điểm của hai đồ thị (P) và (d)
Câu 3: Cho x1,x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
Tính giá trị của biểu thức P = (x1)3 + (x2)3
Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14
a, \(f\left(-2\right)=\dfrac{1}{2}.\left(-2\right)^2=\dfrac{1}{2}.4=2\)
b,
c, Tọa độ giao điểm của 2 đồ thị (P) và (d) thỏa mãn phương trình
\(2x+6=\dfrac{1}{2}x^2\Leftrightarrow x=6;x=-2\)
TH1 : Thay x = 6 vào f(x) ta được : \(\dfrac{1}{2}.6^2=18\)
TH2 : Thay x = -2 vào f(x) ta được : \(\dfrac{1}{2}.\left(-2\right)^2=2\)
Vậy tọa độ giao điểm của (P) và (d) là \(\left(6;18\right);\left(-2;2\right)\)