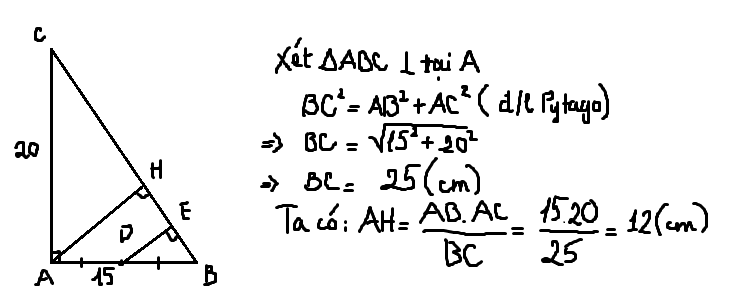cho tam giác ABC vuông tại A, AB = 15cm và AC = 20cm . Gọi M là trung điểm của BC. Tính AM
ST
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, AB = 15cm và AC = 20cm . Gọi M là trung điểm của BC. Tính AM
Áp dụng định lý Py - ta - go vào tam giác vuông ABC, ta có:
AB2 + AC2 = BC2
152 + 202 = BC2
\(\Rightarrow BC=\sqrt{625}=25cm\)
\(\Rightarrow AM=\dfrac{BC}{2}=\dfrac{25}{2}=12,5cm\)
Đúng 1
Bình luận (1)
cho tam giác vuông ABC vuông tại A, AB=15cm, AC=20cm. Gọi M là trung điểm của BC. tính AM
áp dụng định lí py ta go vào tam giác vuông abc vuông tại a . ta có
bc2 = ab2 + ac2
\(\Rightarrow\)bc2 = 152 + 202
\(\Rightarrow\)bc2 = 225 + 400
\(\Rightarrow\)bc2 = 625 = 252
\(\Rightarrow\)bc = 25
vi bm = mc \(\Rightarrow\)am là đường trung tuyến của bc(1)
mà tam giác abc vuông tại a (2)
tu 1 va 2 \(\Rightarrow\)am = 1/2 bc = 1/2 25 = 12,5 ( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại có đường cao AH
a) Chứng minh tam giác AHC đồng dạng với tam giác BHA
b) Cho AB= 15cm AC=20cm. Tính độ dài BC và AH
c) Gọi M là trung điểm của BH và N là trung điểm của AH. C/m CN vuông góc với AM
Sao ý A nhiều ng bảo ko làm đc nhỉ???
Ta chỉ cần dùng tính chất bắc cầu là ra mà
cho tam giác abc vuông tại a (ab<ac),đường cao ah
a)cho ab=15cm ac=20cm tính bc và ah
b)gọi m là trung điểm ab o là trung điểm ac chứng minh h thuộc đường kính ac và mh là tiếp tuyến cùa(O)
Bài 1:Cho tam giác ABC vuông tại A, đường cao AH và AB = 15cm, AC = 20cm. Gọi D là trung điểm của AB. Qua D kẻ DE vuông góc với BC tại E.
a) Tính BC, AH
a:\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 15cm; AC 20cm. Gọi D là trung điểm AB và M là trung điểm BC.Tính BC và DM.Gọi I là trung điểm MD và E là trung điểm AC. Chứng minh: BDEM là hình bình hành và B, I, E thẳng hàng.Gọi O là giao điểm của AM và DE, gọi N là trung điểm BD. Chứng minh: Tứ giác AOIN là hình thang cân.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 15cm; AC = 20cm. Gọi D là trung điểm AB và M là trung điểm BC.
Tính BC và DM.
Gọi I là trung điểm MD và E là trung điểm AC. Chứng minh: BDEM là hình bình hành và B, I, E thẳng hàng.
Gọi O là giao điểm của AM và DE, gọi N là trung điểm BD. Chứng minh: Tứ giác AOIN là hình thang cân.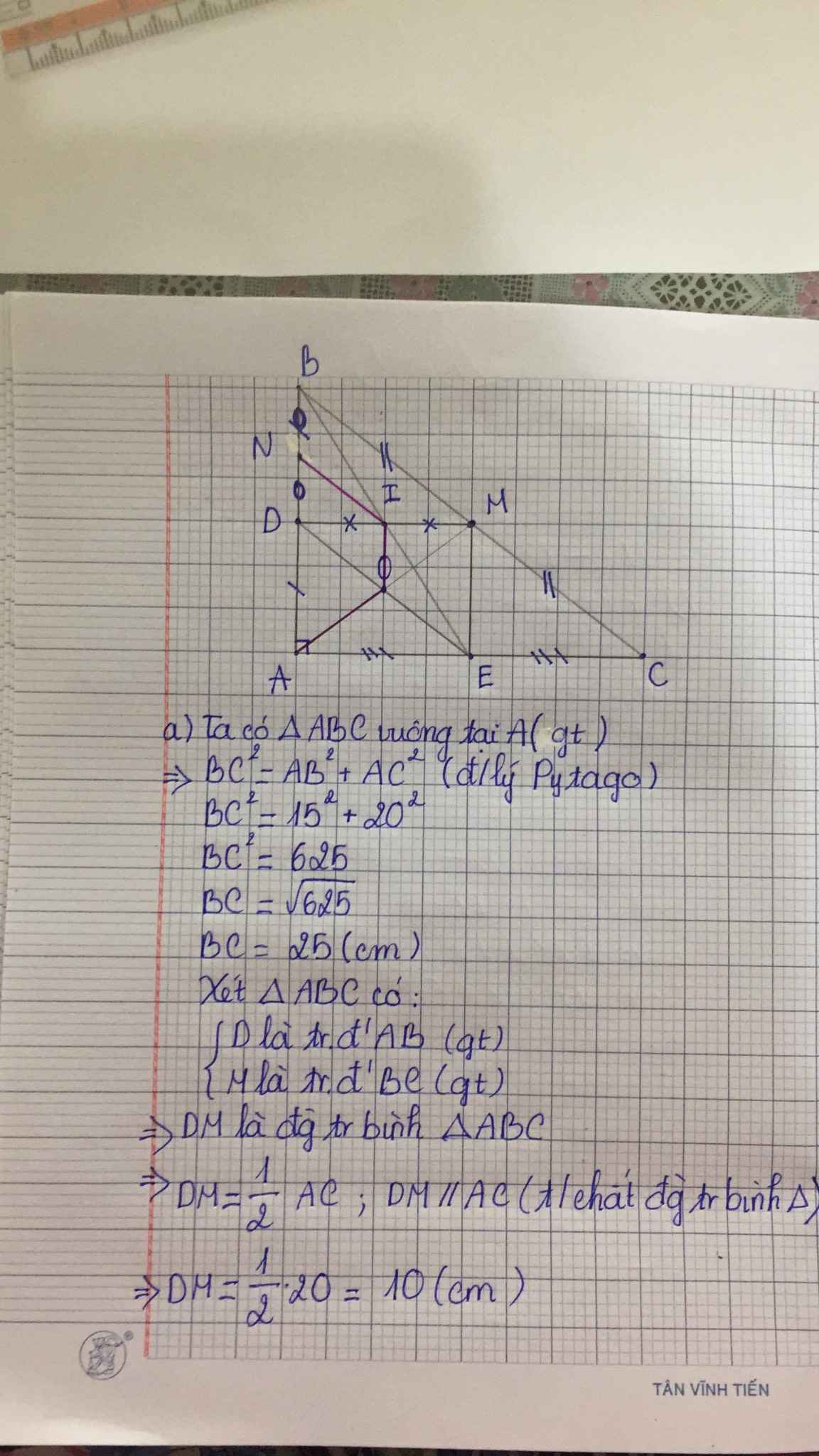

a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=25(cm)
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình của ΔABC
Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH
a. Chứng minh tam giác AHC đồng dạng tam giác BHA
b, Cho AB=15cm, AC=20cm. Tính độ dài BC, AH
c, Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN vuông góc AM
Chứng minh câu a)
Ta có: AH vuông góc với BC ( giả thiết)
=> góc H = 1v
Xét tam giác AHC và tam giác BHA có:
góc AHC=AHB=90 độ
góc B=góc C=45 độ
=>2 tam giác đồng dạng
Câu b)
*BC=?
Ta có tam giác ABC vuông tại A( theo giả thiết0
Theo định lí pi ta go, ta có :
BC^2=AC^2+AB^2=400+225=625
=>BC=25
*AH=?
S tam giác ABC=1/2.AB.AC hoặc 1/2BC.AH
=>AB.AC=BC.AH =>AB/BC=AH/AC
=>AH=15.20/25=12
Câu c)mk ko piet giai nha sorry nha
Đúng 0
Bình luận (1)
Cho tam giác abc vuông tại a có đường cao ah gọi e,f lần lượt là trung điểm ah và bh cho ab=15cm ac =20cm
a) tình bc,ah,hc
b) c/m tam giác bfa đồng dạng tam giác aec
c) c/m af vuông góc với ce và tính en biết n là giao điểm của ef và ac
d) tính diện tích tam giác AEF
Xem chi tiết
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot25=15\cdot20\)
\(\Leftrightarrow AH\cdot25=300\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Vậy: BC=20cm; AH=12cm; HC=16cm
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm và đường cao AH. Vẽ HD vuông góc AB tại D và HE vuông góc AC tại E. a) Vẽ tia vuông góc DE cắt BC tại M. Chứng minh M là trung điểm BC. b) Tính diện tích tam giác ADE
a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc MAC+góc AED=90 độ
=>góc MAC+góc AHD=90 độ
=>góc MAC+góc B=90 độ
=>góc MAC=góc MCA và góc MAB=góc MBA
=>MA=MB=MC
=>M là trung điểm của BC
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=20^2/25=16(cm)
AD=12^2/15=144/15=9,6cm
AE=12^2/20=7,2cm
\(S_{ADE}=\dfrac{1}{2}\cdot7.2\cdot9.6=34.56\left(cm^2\right)\)
Đúng 1
Bình luận (1)