Áp dụng định lý Py - ta - go vào tam giác vuông ABC, ta có:
AB2 + AC2 = BC2
152 + 202 = BC2
\(\Rightarrow BC=\sqrt{625}=25cm\)
\(\Rightarrow AM=\dfrac{BC}{2}=\dfrac{25}{2}=12,5cm\)
cho tam giác ABC vuông tại A, AB = 15cm và AC = 20cm . Gọi M là trung điểm của BC. Tính AM
cho tam giác vuông ABC vuông tại A, AB=15cm, AC=20cm. Gọi M là trung điểm của BC. tính AM
Cho tam giác ABC vuông tại có đường cao AH
a) Chứng minh tam giác AHC đồng dạng với tam giác BHA
b) Cho AB= 15cm AC=20cm. Tính độ dài BC và AH
c) Gọi M là trung điểm của BH và N là trung điểm của AH. C/m CN vuông góc với AM
Cho tam giác ABC vuông tại A có AB = 15cm; AC = 20cm. Gọi D là trung điểm AB và M là trung điểm BC.
Tính BC và DM.
Gọi I là trung điểm MD và E là trung điểm AC. Chứng minh: BDEM là hình bình hành và B, I, E thẳng hàng.
Gọi O là giao điểm của AM và DE, gọi N là trung điểm BD. Chứng minh: Tứ giác AOIN là hình thang cân.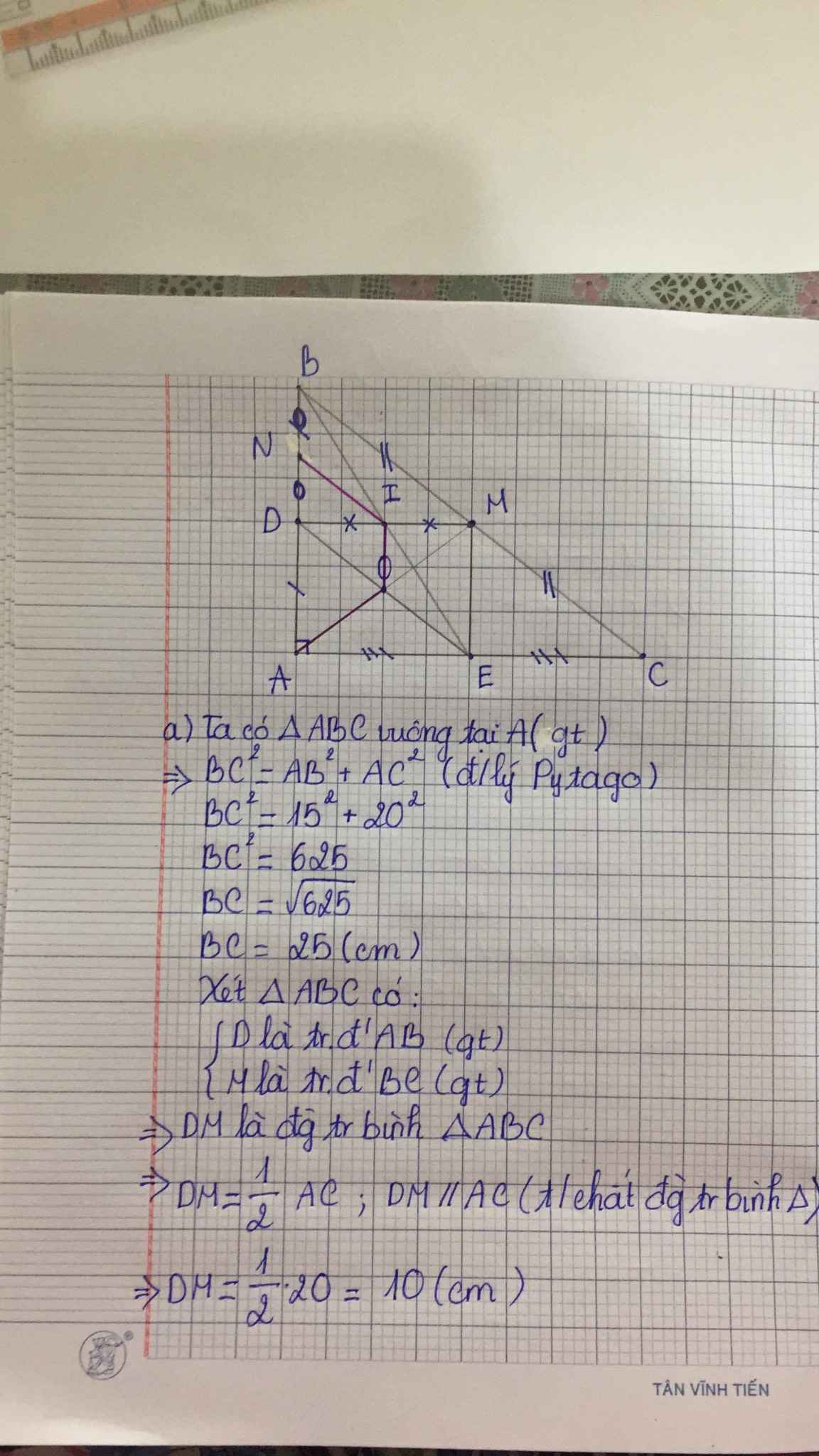
Cho tam giác ABC vuông tại A đường cao AH
a. Chứng minh tam giác AHC đồng dạng tam giác BHA
b, Cho AB=15cm, AC=20cm. Tính độ dài BC, AH
c, Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN vuông góc AM
Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm và đường cao AH. Vẽ HD vuông góc AB tại D và HE vuông góc AC tại E. a) Vẽ tia vuông góc DE cắt BC tại M. Chứng minh M là trung điểm BC. b) Tính diện tích tam giác ADE
cho tam giác abc vuông tại a đường cao ah và ab = 15cm, ac = 20cm. Gọi d là trung điểm của ab, qua d kẻ de vuông góc với bc tại e
a) tính bc, ah
b)chứng tỏ tam giác bde và bah đồng dạng
c) tính de
cho tam giác abc vuông tại a có ab=15cm,bc=25cm.kẻ đường cao ah(h thuộc bc).a) tính độ dài ac.b) kẻ hd vuông với ac(d thuộc ac) và he vuông với ab9e thuộc ab.chứng minh tam giác ade đồng dạng với tam giác abc.c) gọi m là trung điểm của bc.chứng minh am vuông góc với de
