Giúp mình bài này ạ.cảm ơn
VM
Những câu hỏi liên quan
Bạn nào có thể làm làm giúp mình bài này đc ko ạ.Cảm ơn!
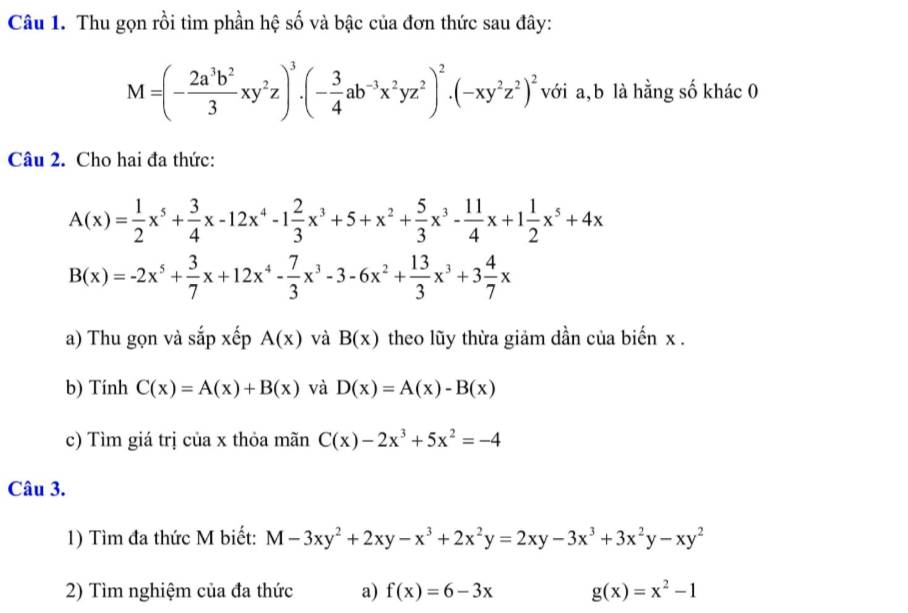
Câu 1.
\(M=\left(-\dfrac{2a^3b^2}{3}xy^2z\right)^3.\left(-\dfrac{3}{4}ab^{-3}x^2yz^2\right)^2.\left(-xy^2z^2\right)^2\)
\(=\left(-\dfrac{8}{27}a^9b^6x^3y^6z^3\right).\left(\dfrac{9}{16}a^2b^{-6}x^4y^2z^4\right).\left(x^2y^4z^4\right)\)
\(=-\dfrac{8}{27}.\dfrac{9}{16}.a^{11}x^9y^{12}z^{11}\)
\(=-\dfrac{1}{6}a^{11}x^9y^{12}z^{11}\)
Hệ số: \(-\dfrac{1}{6}\)
Bậc: \(43\)
Câu 2.
a) \(A\left(x\right)=\dfrac{1}{2}x^5+\dfrac{3}{4}x-12x^4-1\dfrac{2}{3}x^3+5+x^2+\dfrac{5}{3}x^3-\dfrac{11}{4}x+1\dfrac{1}{2}x^5+4x\)
\(=\left(\dfrac{1}{2}x^5+\dfrac{3}{2}x^5\right)+\left(-12x^4\right)+\left(-\dfrac{5}{3}x^3+\dfrac{5}{3}x^3\right)+x^2+\left(\dfrac{3}{4}x-\dfrac{11}{4}x+4x\right)+5\)
\(=2x^5-12x^4+x^2+2x+5\)
\(B\left(x\right)=-2x^5+\dfrac{3}{7}x+12x^4-\dfrac{7}{3}x^3-3-6x^2+\dfrac{13}{3}x^3+3\dfrac{4}{7}x\)
\(=\left(-2x^5\right)+12x^4+\left(-\dfrac{7}{3}x^3+\dfrac{13}{3}x^3\right)-6x^2+\left(\dfrac{3}{7}x+\dfrac{25}{7}x\right)-3\)
\(=-2x^5+12x^4+2x^3-6x^2+4x-3\)
b) \(C\left(x\right)=A\left(x\right)+B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)+\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5-2x^5\right)+\left(-12x^4+12x^4\right)+2x^3+\left(x^2-6x^2\right)+\left(2x+4x\right)+\left(5-3\right)\)
\(=2x^3-5x^2+6x+2\)
\(D\left(x\right)=A\left(x\right)-B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)-\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5+2x^5\right)+\left(-12x^4-12x^4\right)-2x^3+\left(x^2+6x^2\right)+\left(2x-4x\right)+\left(5+3\right)\)
\(=4x^5-24x^4-2x^3+7x^2-2x+8\)
c) \(2x^3-5x^2+6x+2-2x^3+5x^2=-4\)
\(\Rightarrow\left(2x^3-2x^3\right)+\left(-5x^2+5x^2\right)+6x+2\)
\(\Rightarrow6x+2=-4\)
\(\Rightarrow6x=-6\)
\(\Rightarrow x=-1\)
Câu 3.
1) \(M-3xy^2+2xy-x^3+2x^2y=2xy-3x^3+3x^2y-xy^2\)
\(\Rightarrow M=\left(3xy^2+2xy-x^3+2x^2y\right)+\left(2xy-3x^3+3x^2y-xy^2\right)\)
\(=\left(3xy^2-xy^2\right)+\left(2xy+2xy\right)+\left(-x^3-3x^3\right)+\left(2x^2y+3x^2y\right)\)
\(=2xy^2+4xy-4x^3+5x^2y\)
2)
Để cho \(f\left(x\right)\) có nghiệm thì \(6-3x=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Để cho \(g\left(x\right)\) có nghiệm thì \(x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giúp tớ bài này với ạ.Cảm ơn ạ
giúp mình đề này với ạ.Cảm ơn !

 Giúp mình bài II với ạ.Cảm ơn
Giúp mình bài II với ạ.Cảm ơn
Mọi người ơi giúp mình giải bài 7 tiếng việt với ạ.cảm ơn
Xem thêm câu trả lời
Giải mình nốt câu này ạ.cảm ơn
m Na =\(\dfrac{4,6}{23}\)=0,2 mol
2Na+Cl2->2NaCl
0,2---0,1-----0,2
=>VCl2=0,1.22,4=2,24l
=>mNaCl=0,2.58,5=11,7g
Đúng 0
Bình luận (0)
Phân tích nhân vật An Dương Vương trong truyền thuyết An Dương Vương và Mị Châu -Trọng Thuỷ ,từ đó rút ra bài học giữ nước mà tác giả dân gian gửi gắm?
y/c:Lập dàn ý chi tiết
Các bạn giúp mình làm bài tập này với á,vì mik cần gấp lắm ấy ạ.Cảm ơn các bạn trước nha🌻🌸🌺🥰🥰💝🌿🌿
Giúp mk bài 5 và bài 6 đc k ạ.Cảm ơn
Câu 6:
\(B=\left(\dfrac{1}{199}+1\right)+\left(\dfrac{2}{198}+1\right)+...+\left(\dfrac{198}{2}+1\right)+1\)
\(=\dfrac{200}{199}+\dfrac{200}{198}+...+\dfrac{200}{2}+\dfrac{200}{200}\)
\(=200\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{198}+\dfrac{1}{199}\right)\)
=200A
=>A/B=1/200
Đúng 0
Bình luận (0)
Giúp mk bài 5,6 đc ko ạ.Cảm ơn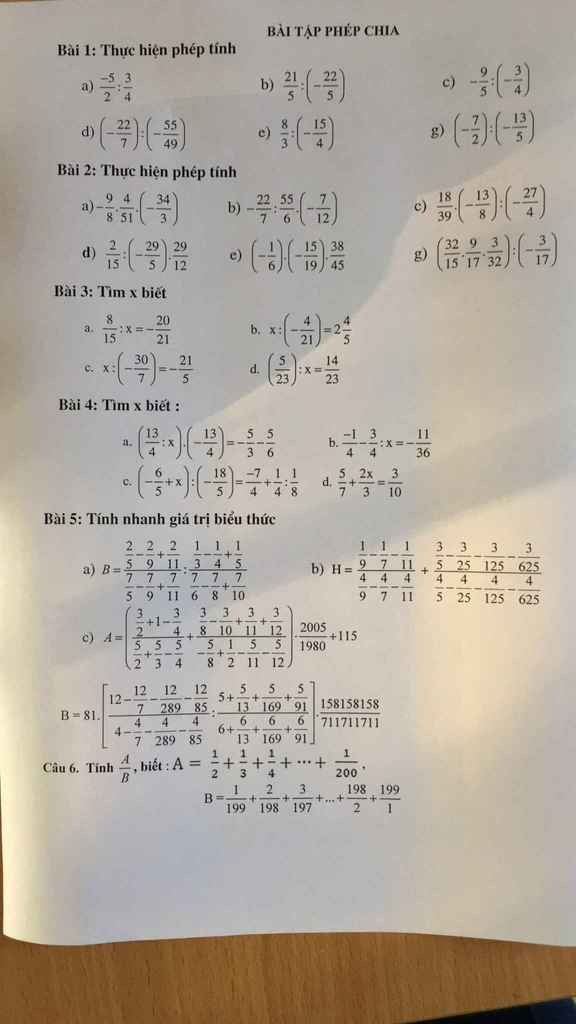
Bài 6:
\(B=\dfrac{1}{199}+1+\dfrac{2}{198}+1+\dfrac{3}{197}+1+...+\dfrac{198}{2}+1+1\)
\(=\dfrac{200}{199}+\dfrac{200}{198}+...+\dfrac{200}{2}+\dfrac{200}{200}\)
\(=200\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{200}\right)=200\cdot A\)
=>A/B=1/200
Đúng 0
Bình luận (1)







