x và y là 2 đại lương tỉ lệ thuận khi x=6, y=4
a) Tìm hệ số tỉ lệ y đối với x
b)Tính y khi x=9
c)Tính x khi y=-3
Bài 1: Đại lượng tỷ lệ thuận
a) x và y là 2 đại lượng tỉ lệ thuận nên ta có hệ số tỉ lệ (k) y đối với x là :
\(y=k.x\Rightarrow k=\dfrac{y}{x}=\dfrac{4}{6}=\dfrac{2}{3}\)
b) Với x=9 ta có :
\(y=\dfrac{2}{3}x=\dfrac{2}{3}.9=6\)
Vậy \(x=9;y=6\)
c) Với y=-3 ta có :
\(y=\dfrac{2}{3}x\Rightarrow x=\dfrac{3y}{2}=\dfrac{3.\left(-3\right)}{2}=-\dfrac{9}{2}\)
Vậy \(y=-3;x=-\dfrac{9}{2}\)
Đúng 1
Bình luận (0)
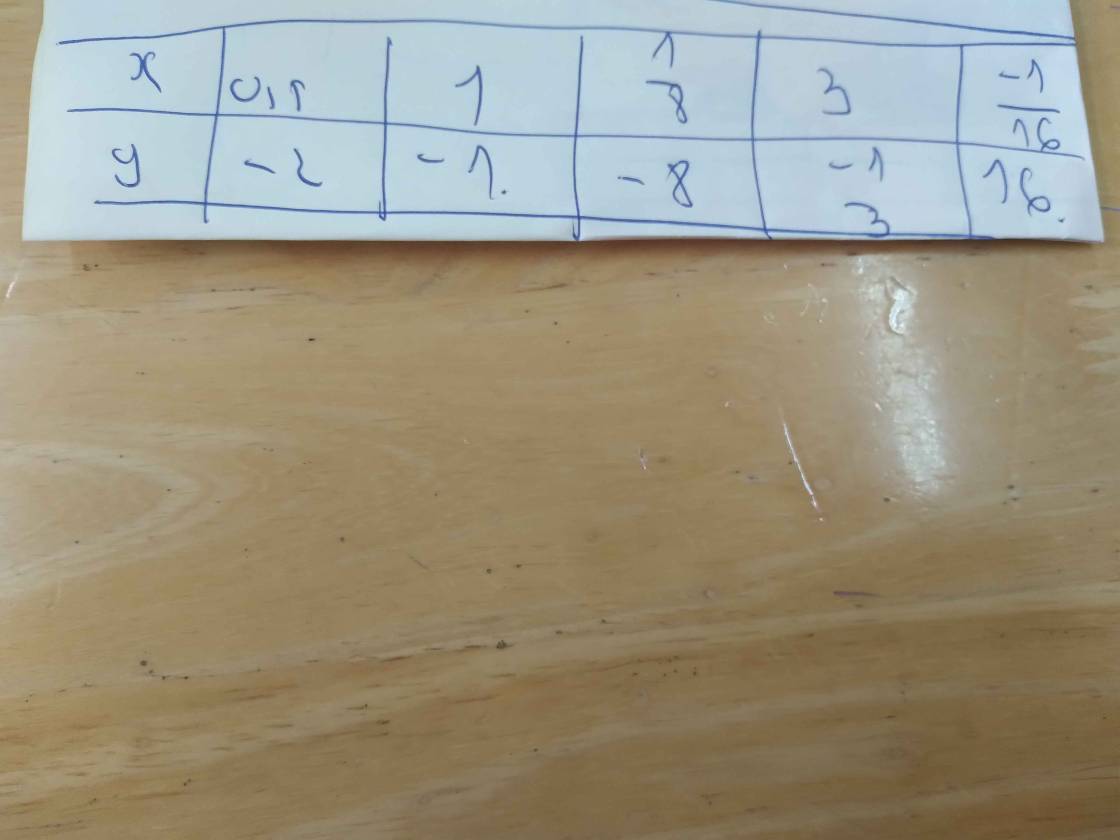
Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào ô trống trong bảng sau:x 0,5 1 3 y -2 -8- 16
Đọc tiếp
Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào ô trống trong bảng sau:
| x | 0,5 | 1 | 3 | ||
| y | -2 | -8 | - | 16 |
Bài 3.
Cho biết x và y là hai đại lượng tỉ lệ thuận. Tìm hệ số tỉ lệ y đối với x biết rằng
1. Với hai giá trị x1, x2 của x có tổng nhận giá trị bằng 8 thì hai giá trị tương ứng vị, và có tổng bằng 4.
2. Với hai giá trị x1, x2 của x có hiệu x₁ - x₁ = 3 thì hai giá trị tương ứng Vị, và có cho hiệu V1-V2=6.
1: x và y tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(x_1+x_2=8;y_1+y_2=4\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{8}{4}=2\)
=>x=2y
=>\(y=\dfrac{1}{2}x\)
=>Hệ số tỉ lệ của y đối với x là 1/2
2: \(x_1-x_2=3;y_1-y_2=6\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1-x_2}{y_1-y_2}=\dfrac{3}{6}=\dfrac{1}{2}\)
=>y=2x
=>Hệ số tỉ lệ của y đối với x là 2
Đúng 2
Bình luận (0)
Cho x y là hai đại lượng tỉ lệ thuận và x1 - x2 =3 ; y1 - y2 =9 a) hãy biểu diễn y theo x b) tính giá trị của x khi y = 12
Do x và y là hai đại lượng tỉ lệ thuận nên ta đặt: \(\dfrac{y}{x}=\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=k\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=\dfrac{y_1-y_2}{x_1-x_2}=\dfrac{9}{3}=3\)
\(\Rightarrow k=3\)
\(\Rightarrow\dfrac{y}{x}=3\Rightarrow y=3x\)
Nếu `y=12` thì:
\(3x=12\Rightarrow x=\dfrac{12}{3}=4\)
Đúng 1
Bình luận (0)
Cho x y là 2 đại lượng tỉ lệ thuận và x1 +x2 = 5 ; y1 +y2= 10 Hãy biểu diễn y theo x Tính giá trị của x khi y = -10
Cho x y là 2 đại lượng tỉ lệ thuận và x1 + x2 =5 ; y1 + y2=10 Hãy biểu diễn y theo x Tính giá trị của x khi y = -10
Do x và y là hai đại lượng tỉ lệ thuận nên ta đặt: \(\dfrac{y}{x}=\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=k\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=\dfrac{y_1+y_2}{x_1+x_2}=\dfrac{10}{5}=2\)
\(\Rightarrow k=2\)
\(\Rightarrow\dfrac{y}{x}=2\Rightarrow y=2x\)
Nếu `y=-10` thì:
\(2x=-10\Rightarrow x=\dfrac{-10}{2}=-5\)
Đúng 1
Bình luận (0)
Cho x và y là hzi dại lượnh tỉ lệ nghịch gọi x1,x2 là hai giá trị của x vag y1,y2 là hai giá trị tương ứng của y biết x1=14,x2=21 và y2 =3 tính y1,y2 biểu diễn y theo x và tính giá trị xkhi y=-3
x,y là hai đại lượng tỉ lệ nghịch
=>\(x_1\cdot y_1=x_2\cdot y_2\)
=>\(14\cdot y_1=21\cdot3=63\)
=>\(y_1=4,5\)
=>\(k=x_1\cdot y_1=14\cdot4,5=63\)
Ta có: xy=k
=>xy=63
=>\(y=\dfrac{63}{x}\)
Thay y=-3 vào y=63/x, ta được:
\(\dfrac{63}{x}=-3\)
=>\(x=-\dfrac{63}{3}=-21\)
Đúng 1
Bình luận (0)
Ví dụ 4: Cho x, y là hai đại lượng tỉ lệ thuận với nhau, x1; x2 là hai giá trị của x và y1; y2 là hai
giá trị tương ứng của y. Biết 2y1 + 3x1 = 22; x2 = 4; y2 = 16. Khi đó giá trị của x1 là bao nhiêu?
A. x1 = 8 B. x1 = −8 C. x1 = −2 D. x1 = 2
x,y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{4}=\dfrac{y_1}{16}\)
=>\(\dfrac{x_1}{1}=\dfrac{y_1}{4}\)
mà \(3x_1+2y_1=22\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{1}=\dfrac{y_1}{4}=\dfrac{3x_1+2y_1}{3\cdot1+2\cdot4}=\dfrac{22}{11}=2\)
=>\(x_1=2\cdot1=2\)
=>Chọn D
Đúng 0
Bình luận (0)
Cho x, y là hai đại lượng tỉ lệ thuận với nhau. Gọi x1, 2 là hai giá trị của x và y1, y2 là hai giá trị tương ứng của y. Biết rằng x1 + x2 = -3 và y1 + y2 = 15
a) Tìm hệ số tỉ lệ của y đối với x
b) Tính các giá trị của x khi y = -2 và y = -9
a: x và y tỉ lệ thuận với nhau
=>\(\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=\dfrac{y_1+y_2}{x_1+x_2}=\dfrac{15}{-3}=-5\)
=>y=-5x
b: y=-5x
=>\(x=-\dfrac{1}{5}y\)
Thay y=-2 vào \(x=-\dfrac{1}{5}y\), ta được:
\(x=-\dfrac{1}{5}\cdot\left(-2\right)=\dfrac{2}{5}\)
Thay y=-9 vào x=-1/5y, ta được:
\(x=-\dfrac{1}{5}\cdot\left(-9\right)=\dfrac{9}{5}\)
Đúng 1
Bình luận (0)
cho dãy tỉ số a/b = c/d. Chứng minh a2+c2/b2+d2 =ac/bd sos
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{b}.\dfrac{a}{b}=\dfrac{c}{d}.\dfrac{c}{d}=\dfrac{a}{b}.\dfrac{c}{d}\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)
Đúng 0
Bình luận (0)