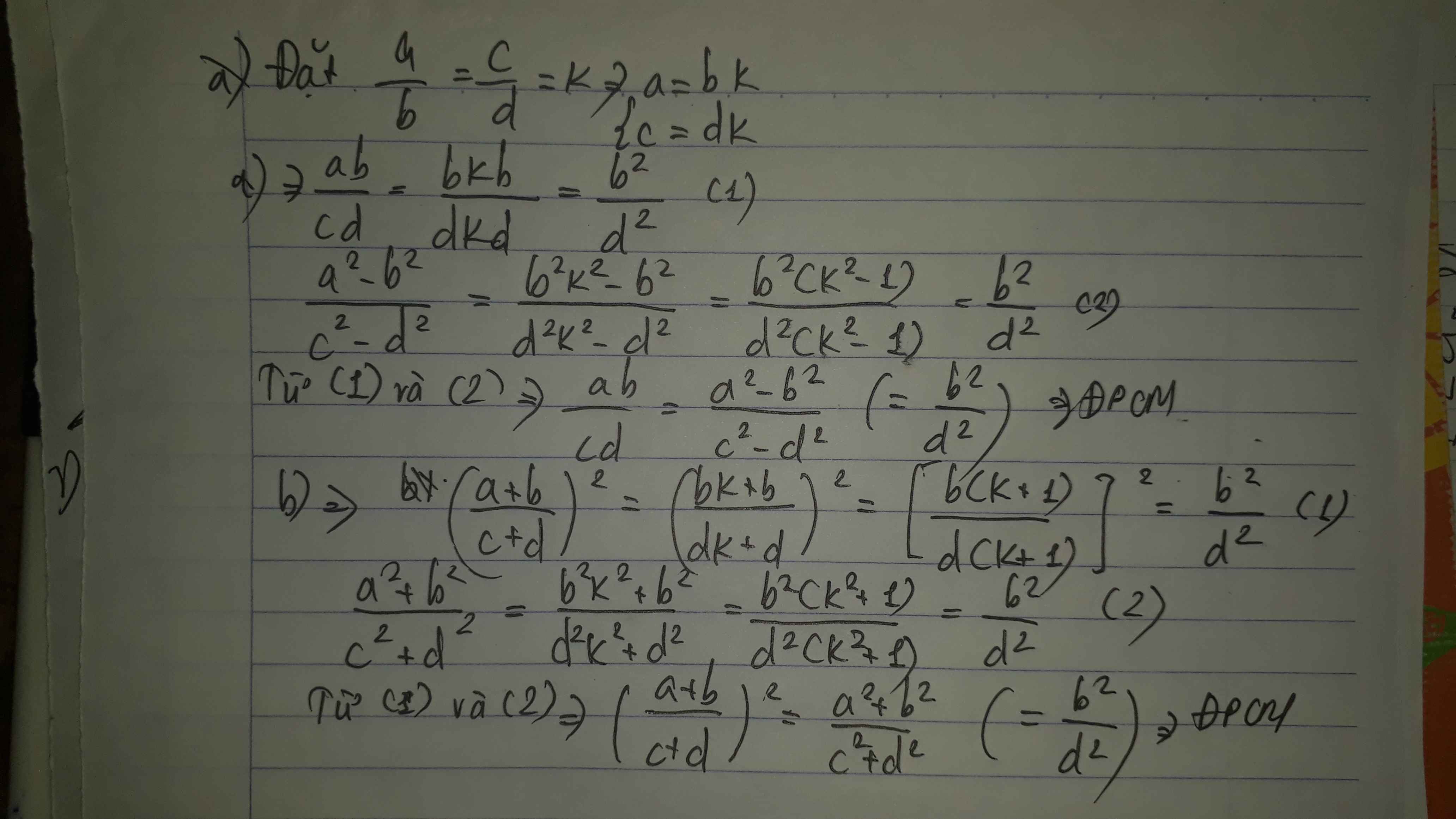Cho tỉ lệ thức a/b=c/d. Chứng minh rằng: ab/cd=a^2-b^2/c^2-d^2 và (a+b/c+d)=a^2+b^2/c^2+d^2
NT
Những câu hỏi liên quan
Cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. Chứng minh rằng a/b=c/d
Cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. Chứng minh rằng a/b=c/d
Đặt
Khi đó ta có :
và
Suy ra :
Ta lại có :
Đúng 1
Bình luận (0)
Đặt
Khi đó ta có :
và
Suy ra :
Ta lại có :
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức là có nghĩa ) :
a) \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b) \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
Cho tỉ lệ thức a/b = c/d . Chứng minh rằng ab/cd = ( a - b ) ^ 2 / ( c - d ) ^2
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt$. Ta có:
$\frac{ab}{cd}=\frac{b^2t}{d^2t}=\frac{b^2}{d^2}(1)$
Mặt khác:
$\frac{(a-b)^2}{(c-d)^2}=\frac{(bt-b)^2}{(dt-d)^2}=\frac{b^2(t-1)^2}{d^2(t-1)^2}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)\Rightarrow \frac{ab}{cd}=\frac{(a-b)^2}{(c-d)^2}$
Đúng 0
Bình luận (0)
cho tỉ lệ thức a^2+b^2/c^2+d^2=ab/cd. chứng minh rằng a/b=c/d
Cho tỉ lệ thức : a/b = c/d ( a , b , c , d khác 0 )
Chứng minh rằng : a^2 + b^2 / c^2 + d^2 = ab / cd
\(\frac{a}{b}=\frac{c}{d}\)
=> \(\frac{a}{c}=\frac{b}{d}\)
=> \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}\)(Tính chất dãy tỉ số bằng nhau)
=> \(\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}\)(Đpcm)
Đúng 0
Bình luận (0)
Cho tỉ lệ thức a/b=b/c chứng minh rằng :
1.a-b/b=c-d/d
2.ab/cd=(a-d)^2/(c-d)^2
1, a) \(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow\frac{a}{c}=\frac{b}{d}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
=> b(c-d)=d(a-b)
=> \(\frac{c-d}{d}=\frac{a-b}{b}\)(đpcm)
2, Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2k}{d^2k}=\frac{b^2}{d^2}\) (1)
Mặt khác: \(\frac{\left(a-b\right)^2}{\left(c-d\right)^2}=\frac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\frac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\frac{b^2}{d^2}\)(2)
Từ (1) và (2) => \(\frac{ab}{cd}=\frac{\left(a-b\right)^2}{\left(c-d\right)^2}\)(đpcm)
Hình như đề của bạn sai 1 số chỗ
Đúng 0
Bình luận (0)
cho tỉ lệ thức a/b = c/d. chứng minh các tỉ lệ thức sau a^2-b^2 / ab = c^2-d^2/cd ,
Lần sau bạn cho thêm cả dấu ngoặc cho dễ hiểu nhé :v
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) \(\left(b,d\ne0\right)\)
Thay \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) vào \(\frac{a^2-b^2}{ab}\) và \(\frac{c^2-d^2}{cd}\) ta có :
\(\left\{{}\begin{matrix}\frac{\left(b.k\right)^2-b^2}{b.k.b}\\\frac{\left(d.k\right)^2-d^2}{d.k.d}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2.k^2-b^2}{b^2.k}\\\frac{d^2.k^2-d^2}{d^2.k}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2\left(k^2-1\right)}{b^2.k}\\\frac{d^2\left(k^2-1\right)}{d^2.k}\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}\frac{k^2-1}{k}\\\frac{k^2-1}{k}\end{matrix}\right.\)(vì b,d khác 0 nên \(b^2,d^2\) khác 0)
=> \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) (vì cùng bằng \(\frac{k^2-1}{k}\))
vậy \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) nếu \(\frac{a}{b}=\frac{c}{d}\)
lâu lắm không làm nên không chắc đâu :v
Cho tỉ lệ thức:(a^2+b^2) / (c^2+d^2) = ab/cd . chứng minh : a/b=c/d hoặc a/b=d/c (chứng minh 1 trong 2 )?
(a² + b²) / (c² + d²) = ab/cd
<=> (a² + b²)cd = ab(c² + d²)
<=> a²cd + b²cd = abc² + abd²
<=> a²cd - abc² - abd² + b²cd = 0
<=> ac(ad - bc) - bd(ad - bc) = 0
<=> (ac - bd)(ad - bc) = 0
<=> ac - bd = 0 hoặc ad - bc = 0
<=> ac = bd hoặc ad = bc
<=> a/b = d/c hoặc a/b = c/d (đpcm)
Đúng 1
Bình luận (2)
https://i.imgur.com/ykdB9uk.jpg