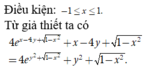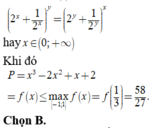a. 

$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$

b.

$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$

c.

$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$

d.

$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$

$=(x+1)(x^2-4x+1)$

e.

$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$

$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$

f.

$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$

$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$

g.

$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$

$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$

$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$

$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$

h.

$x^6+2x^5+x^4-2x^3-2x^2+1$

$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$

$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

a) (x - y)(x + y + 3).                    b) (x + y - 2xy)(2 + y + 2xy).

c) x 2 (x + l)( x 3  -  x 2  + 2).              d) (x – 1 - y)[ ( x   -   1 ) 2   +   ( x   -   1 ) y   +   y 2 ].

Xét hàm  trên  ℝ  và đi đến kết quả 

a) x6 – x4 + 2x3 + 2x2

= x2(x4 – x2 + 2x + 2)

= x2[x2(x2 – 1) + 2(x + 1)]

= x2. [x2.(x -1).(x + 1) + 2(x+ 1)]

= x2 (x+ 1).[x2(x- 1)+ 2]

= x2(x + 1)(x3 – x2 + 2)

= x2(x + 1)[(x3 + 1) – (x2 – 1)]

= x2(x + 1).[(x + 1).(x2 – x + 1) - (x - 1).(x + 1)]

= x2(x + 1)(x + 1)( x2 – x + 1 – x + 1)

= x2(x + 1)2(x2 – 2x + 2).

b) 4x4 + y4 = 4x4 + 4x2y2 + y4 - 4x2y2

= (2x2 + y2)2 - (2xy)2

= (2x2 + y2 + 2xy)(2x2 + y2 - 2xy)

ủa mũ hay để nguyên z?? 

hđt =x^2(x+1)^2(x^2-2x+2)

x⁶ - x⁴ + 2x³ + 2x²

= x²(x⁴ - x² + 2x + 2)

= x²[(x⁴ - x²) + (2x + 2)]

= x²[x²(x² - 1) +2(x + 1)]

= x²[x²(x - 1)(x + 1) + 2(x + 1)]

= x²(x + 1)[x²(x - 1) + 2]

= x²(x + 1)(x³ - x² + 2)

= x²(x + 1)(x³ + x² - 2x² - 2x + 2x + 2)

= x²(x + 1)[(x³ + x²) - (2x² + 2x) + (2x + 2)]

= x²(x + 1)[x²(x + 1) - 2x(x + 1) + 2(x + 1)]

= x²(x + 1)²(x² - 2x + 2)

\(=\left(x^6+2x^5+x^4\right)-2\left(x^5+2x^4+x^3\right)+2\left(x^4+2x^3+x^2\right)\)

\(=x^2\left(x^2+x\right)^2-2x\left(x^2+x\right)^2+2\left(x^2+x\right)^2\)

\(=\left(x^2+x\right)^2\left(x^2-2x+2\right)\)

\(=x^2\left(x+1\right)^2\left(x^2-2x+2\right)\)

\(x^6-x^4+2x^3+2x^2\)

\(=x^2\left(x^4-x^2+2x+2\right)\)

\(=x^2\left[x^2\left(x-1\right)\left(x+1\right)+2\left(x+1\right)\right]\)

\(=x^2\left(x+1\right)\left(x^3-x^2+2\right)\)

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có

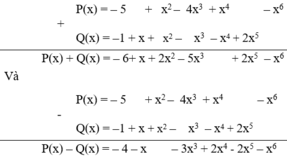
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6

P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6

\(\Leftrightarrow\)\(4y^2+12y=4x^4+4x^2+72\)

\(\Leftrightarrow\left(2y+3\right)^2=\left(2x^2+1\right)^2+80\)

\(\Leftrightarrow\left(2y+3\right)^2-\left(2x^2+1\right)^2=80\)

\(\Leftrightarrow\left(2y+3-2x^2-1\right)\left(2y+3+2x^2+1\right)=80\)

\(\Leftrightarrow\left(y-x^2+1\right)\left(y+x^2+2\right)=20\)

Do \(x,y\in Z\) => \(y+1-x^2;y+x^2+2\in Z\)

=>\(y+1-x^2;y+x^2+2\inƯ\left(20\right)\)

Kẻ bảng làm nốt nha.

Ta có (1)  ⇔ x 4 + x 2 + 20 = y 2 + y

Ta thấy:  x 4 + x 2 < x 4 + x 2 + 20 ≤ x 4 + x 2 + 20 + 8 x 2 ⇔ x 2 ( x 2 + 1 ) < y ( y + 1 ) ≤ ( x 2 + 4 ) ( x 2 + 5 )

Vì x, y ∈ Z nên ta xét các trường hợp sau

+ TH1.  y ( y + 1 ) = ( x 2 + 1 ) ( x 2 + 2 ) ⇔ x 4 + x 2 + 20 = x 4 + 3 x 2 + 2 ⇔ 2 x 2 = 18 ⇔ x 2 = 9 ⇔ x = ± 3

Với  x 2 = 9   ⇒ y 2 + y = 9 2 + 9 + 20 ⇔ y 2 + y − 110 = 0 ⇔ y = 10 ; y = − 11 ( t . m )

+ TH2  y ( y + 1 ) = ( x 2 + 2 ) ( x 2 + 3 ) ⇔ x 4 + x 2 + 20 = x 4 + 5 x 2 + 6 ⇔ 4 x 2 = 14 ⇔ x 2 = 7 2   ( l o ạ i )

+ TH3: y ( y + 1 ) = ( x 2 + 3 ) ( x 2 + 4 ) ⇔ 6 x 2 = 8 ⇔ x 2 = 4 3   ( l o ạ i )

+ TH4:  y ( y + 1 ) = ( x 2 + 4 ) ( x 2 + 5 ) ⇔ 8 x 2 = 0 ⇔ x 2 = 0 ⇔ x = 0

Với  x 2 = 0  ta có  y 2 + y = 20 ⇔ y 2 + y − 20 = 0 ⇔ y = − 5 ; y = 4

Vậy PT đã cho có nghiệm nguyên (x;y) là :

(3;10), (3;-11), (-3; 10), (-3;-11), (0; -5), (0;4).