cho tam giác ABC vuông tại A,điểm M và N lần lượt là chung điểm của các cạnh BC,AC;gọi D đối xứng N qua M.tia AM cắt CD tại E.Chứng minh tứ giác BDCN là hình bình hành
ND
Những câu hỏi liên quan
Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Kẻ các đường thẳng song song với cạnh AB, AC lần lượt cắt các cạnh AC, AB tại P và Q.
a) Gọi N là điểm đối xứng của M qua Q. Gỉa sử tam giác ABC vuông tại A. Chứng minh rằng: Tứ giác AMBN là hình thoi.
c) Tam giác ABC có điều kiện giừ để tứu giác AMBN là hình vuông?
a: Xét tứ giác AMBN có
Q là trung điểm của AB
Q là trung điểm của MN
Do đó: AMBN là hình bình hành
mà MA=MB
nên AMBN là hình thoi
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A. Trên cạnh BC lần lượt là BC lần lượt lấy các điểm M và N ( M nằm giữa B và N ) sao cho BM = CN. Kẻ MH vuông góc với AB; NK vuông góc với AC. Chứng minh:
a) Tam giác MHB = tam giác NKC
b) AH = AK
c) tam giác AMN cân tại A
a: Xét ΔMHB vuông tại H và ΔNKC vuông tại K có
BM=CN
\(\widehat{B}=\widehat{C}\)
Do đó: ΔMHB=ΔNKC
b: Ta có: ΔMHB=ΔNKC
nên HB=KC
Ta có: AH+HB=AB
AK+KC=AC
mà BA=AC
và HB=KC
nên AH=AK
c: Xét ΔAHM vuông tại H và ΔAKN vuông tại K có
AH=AK
HM=KN
Do đó: ΔAHM=ΔAKN
Suy ra: AM=AN
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên cạnh AB, AC lần lượt lấy các điểm M, N sao cho góc ABN = góc ACM = 15 độ. Gọi I là giao điểm của MC và NB. Gọi H,E,D lần lượt là trung điểm của BC,BN,CM.
a) So sánh tam giác ABN và tam giác ACM.
b) C/m tam giác ADE đều.
c) C/m 3 điểm A,I,H thẳng hàng.
d) Tính góc DHE
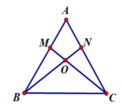
Cho tam giác ABC có ABAC. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AMAN. Nối BN và CM gặp nhau tại O.a)
B
A
C
^
là góc chung của các tam giác nào?b) BC là cạnh chung của các tam giác nào?c) Các cặp góc nào kề bù nhaud) Tìm các tam giác có cạnh là AO
Đọc tiếp
Cho tam giác ABC có AB=AC. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM=AN. Nối BN và CM gặp nhau tại O.
a) B A C ^ là góc chung của các tam giác nào?
b) BC là cạnh chung của các tam giác nào?
c) Các cặp góc nào kề bù nhau
d) Tìm các tam giác có cạnh là AO
cho tam giác abc vuông tại a gọi m,n lần lượt là trung điểm của các cạnh bc và ac gọi e là điểm đối xứng với m qua ab chứng minh aebm là hình thoi
Xét tứ giác AEBM có
Hai đường chéo AB và EM cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau
nên AEBM là hình thoi
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác ABC vuông cân tại A. Trên cạnh AB, AC lần lượt lấy các điểm M, N sao cho 2 góc ABN=ACM 15°. Gọi I là giao điểm của MC và NB. Gọi H, E, D lần lượt là trung điểm của BC, BN,СМ.
a) So sánh 2 tam giác ABN và ACM
b) Chứng minh tam giác ADE đều
c) Chứng minh ba điểm A, I, H thẳng hàng ;
d) Tính: Góc DHE
a: Xét ΔABN vuông tại A và ΔACM vuông tại A có
AB=AC
góc ABN=góc ACM
=>ΔABN=ΔACM
b: ΔABN vuông tại A có AE là trung tuyến
nên AE=BE=NE=BN/2
ΔACM vuông tại A có AD là trung tuyến
nên AD=CM/2=BN/2=AE
góc EAB=góc EBA=15 độ
góc DAC=góc DCA=15 độ
=>góc EAD=90-15-15=60 độ
Xét ΔAED có AE=AD và góc EAD=60 độ
nên ΔAED đều
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
=>IB=IC
=>I nằm trên trung trực của BC
=>A,I,H thẳng hàng
Đúng 0
Bình luận (0)
Bài 5: Cho tam giác ABC vuông tại A,AB12 cm BC13 cm .Gọi M, N lần lượt là trungđiểm của AB và BCa) Chứng minhMN vuông góc AB b) Tính độ dài MNBài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi Ilà giao điểm của AP và MN. C/m: a) IA IP b) IM IN.Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểmcủa DH, M là trung điểm của HC.C/m:a) IM vuông góc AD b) AI vuông góc DM.
Đọc tiếp
Bài 5: Cho tam giác ABC vuông tại A,
AB=12 cm BC=13 cm .
Gọi M, N lần lượt là trung
điểm của AB và BC
a) Chứng minh
MN vuông góc AB
b) Tính độ dài MN
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểm
của DH, M là trung điểm của HC.
C/m:a) IM vuông góc AD b) AI vuông góc DM.
Cho tam giác ABC vuông tại A. Gọi D,E,F lần lượt là trung điểm của các cạnh BC, AB, AC. Chứng minh rằng:
a. DE//AC, DF//AB.
b. Tứ giác AEDF là hình chữ nhật.
c. Gọi M và N lần lượt là các điểm đối xứng với D qua AB và AC. Chứng minh M đối xúng với N qua A.
Để chứng minh các phần a, b và c, ta sẽ sử dụng các tính chất của tam giác vuông và hình chữ nhật.
a. Ta có tam giác ABC vuông tại A, nên theo định lí trung tuyến, ta có DE là đường trung tuyến của tam giác ABC. Do đó, DE song song với cạnh AC. Tương tự, ta có DF song song với cạnh AB. Vậy DE//AC và DF//AB.
b. Ta cần chứng minh AEDF là hình chữ nhật. Đầu tiên, ta thấy DE//AC và DF//AB (theo phần a). Khi đó, ta có:
- AD = DC (vì D là trung điểm của BC)
- AE = EB (vì E là trung điểm của AB)
- AF = FC (vì F là trung điểm của AC)
Vậy ta có các cạnh đối diện của tứ giác AEDF bằng nhau, do đó AEDF là hình chữ nhật.
c. Gọi M là điểm đối xứng của D qua AB. Ta cần chứng minh M đối xứng với N qua A. Để làm điều này, ta sẽ chứng minh AM = AN và góc MAN = góc NAM.
- Vì M là điểm đối xứng của D qua AB, nên ta có AM = AD.
- Vì N là điểm đối xứng của D qua AC, nên ta có AN = AD.
Do đó, ta có AM = AN.
- Ta có góc MAD = góc DAB (vì M là điểm đối xứng của D qua AB)
- Ta có góc NAD = góc DAC (vì N là điểm đối xứng của D qua AC)
Vì tam giác ABC vuông tại A, nên góc DAB = góc DAC. Từ đó, ta có góc MAD = góc NAD.
Vậy ta có AM = AN và góc MAN = góc NAM, do đó M đối xứng với N qua A.
Vậy ta đã chứng minh được M đối xứng với N qua A.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là hình chiếu của điểm H trên các cạnh AB và AC
a, Chứng minh AD . AB = AE . AC
b, Gọi M , N lần lượt là trung điểm của BH và CH . Chứng minh DE là tiếp tuyến chung của 2 đường tròn ( M , MD ) và ( N , NE )
c,Gọi P là trung điểm MN , Q là giao điểm của DE và AH , giả sử AB=6cm , AC=8cm . Tính độ dài PQ
a: XétΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
Đúng 2
Bình luận (0)