Tìm số tự nhiên a cùng với các số 8;17 làm thành độ dài 3 cạnh của 1 tam giác vuông
SS
Những câu hỏi liên quan
1.Chứng minh rằng: Với mọi số tự nhiên các số sau là các số nguyên tố cùng nhau.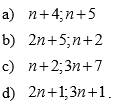
2.Tìm các số tự nhiên để các số sau nguyên tố cùng nhau. 
1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
Đúng 2
Bình luận (0)
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau
Đúng 1
Bình luận (0)
đề 1 chứng minh rằng với mọi số tự nhiên n ,các số sau là số nguyên tố cùng nhau
a/ 7n+10 và 5n+7
b/ 2n+ và 4n+8
đề 2 chứng minh rằng có vô số tự nhiên n để n+15 và n+72 là hai số nguyên tố cùng nhau
Đề 3 số tự nhiên n có 54 ước , Chứng minh rằng tích các ước của n bằng n^27
Đề 4 tìm số tự nhiên khác 0 nhỏ hơn 60 có nhiều ước nhất
đề 1 chứng minh rằng với mọi số tự nhiên n ,các số sau là số nguyên tố cùng nhau
a/ 7n+10 và 5n+7
b/ 2n+ và 4n+8
đề 2 chứng minh rằng có vô số tự nhiên n để n+15 và n+72 là hai số nguyên tố cùng nhau
Đề 3 số tự nhiên n có 54 ước , Chứng minh rằng tích các ước của n bằng n^27
Đề 4 tìm số tự nhiên khác 0 nhỏ hơn 60 có nhiều ước nhất
Cho phân số 51/78.Nếu cùng bớt tử số và mẫu số đi cùng 1 số tự nhiên a ta được phân số mới có giá trị bàng 5/8.Tìm số tự nhiên a
không giúp thi, bn chưa đọc nội quy phòng thi à ?
Đúng 3
Bình luận (0)
Cho phân số 51/78.Nếu cùng bớt tử số và mẫu số đi cùng 1 là
78 - 51 = 27
tử số là 5. còn mẫu là 8
tử mới
: 27 : ( 8-5) x 5 = 45
số càn tìm
51 - 45 = 6
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
cho ps 51/78.nếu cùng bớt ở tử số và mẫu số đi cùng 1 số tự nhiên a thì ta đc ps mới có giá trị = 5/8 .Tìm số tự nhiên a
TK
Nếu bớt mẫu số và tử số cùng 1 số tự nhiên thì hiệu phân số cũ không thay đổi và bằng :
78 - 51 = 27
Coi tử số mới là 5 phần thì mẫu số mới là 8 phần
Tử số mới là :
27 : ( 8 - 5 ) x 5 = 45
=> Số cần tìm là :
51 - 45 = 6
Đáp số : 6
Đúng 1
Bình luận (4)
Cho phân số 51/78. Nếu cùng bớt ở tử số và mẫu số đi cùng một số tự nhiên ad9uoc75 phân số mới có giá trị bằng 5/8. Tìm số tự nhiên a
\(\dfrac{51-a}{78-a}=\dfrac{5}{8}\)
\(⇔ 5 × ( 78 − a ) = 8 × ( 51 − a )\)
\(⇔ 390 − 5 a = 408 − 8 a\)
\( 3 a = 18\)
\(a=18:3\)
\(a=6\)
Đúng 1
Bình luận (4)
a) CMR:với n là số tự nhiên thì 2n+3 và 6n+8 là hai số nguyên tố cùng nhau
b)Tìm tất cả các số tự nhiên n để 3n + 12 là số nguyên tố
Cho phân số 51/78. Nếu cùng bớt ở tử số và mẫu số đi cùng một số tự nhiên a thì ta được phân số mới có giá trị bằng 5/8. Tìm số tự nhiên a.
Hiệu của MS và TS là:
78-51=27
Nếu coi TS là 5 phần thì MS là 8 phần
TS mới là:
27:(8-5)x5=45
Số tự nhiên a là:
51-45=6
Đ/S:6
Đúng 2
Bình luận (0)
= 6
:(((
......
Cho phân số 51/78.Nếu cùng bớt ở tử số và mẫu số đi cùng một số tự nhiên a thì ta được phân số mới có giá trị bằng 5/8.Tìm số tự nhiên a.
nếu bớt cả tử và mẫu số của một phân số đi cùng 1 số thì hiệu 2 không thay đổi , vậy hiệu mẫu và tử số là :
78-51=27
tỉ số là 5/8,tử số sau khi thêm là :
27:(8-5)*5=45
số a là :51-45=6
ĐS: số a là 6
Đúng 0
Bình luận (0)
a) chứng minh rằng khi nla số tự nhiên khác 0 thì n+1 là 2 số nguyên tố cùng nhau.
b)chứng minh rằng với mọi số tự nhiên n thì các số sau là nguyên tố cùng nhau :2n+3 va 4n+8
e có 2 chia hết cho d; 2n+3 lẻ nên (2n+3,4n+8)=1
còn n+1-n=1 nên (n,n+1)=1








