Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số : \(\dfrac{V_{\left(H\right)}}{V_{ABCD}}\) ?

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi G_1,G_2,G_3 lần lượt là trọng tâm các tam giác ABC, ACD, ADBa) Chứng minh left(G_1G_2G_3right)//left(BCDright)b)Tìm thiết diện của tứ diện ABCD với mp left(G_1G_2G_3right). Tính diện tích thiết diện khi biết diện tích tam giác BCD là Sc) M là điểm di động bên trong tứ diện sao cho GM luôn song song với mặt phẳng (ACD). Tìm tập hợp những điểm M
Đọc tiếp
Cho tứ diện ABCD. Gọi \(G_1,G_2,G_3\) lần lượt là trọng tâm các tam giác ABC, ACD, ADB
a) Chứng minh \(\left(G_1G_2G_3\right)//\left(BCD\right)\)
b)Tìm thiết diện của tứ diện ABCD với mp \(\left(G_1G_2G_3\right)\). Tính diện tích thiết diện khi biết diện tích tam giác BCD là S
c) M là điểm di động bên trong tứ diện sao cho GM luôn song song với mặt phẳng (ACD). Tìm tập hợp những điểm M
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB a; AC a
2
; AD a
3
,(a0) Thể tích V của khối tứ diện ABCD là: A.
V
a
3
6
3
B. ...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Đáp án B
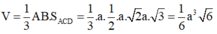
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có BCa, CDa
3
,
B
C
D
^
A
B
C
^
A
D
C
^
90
°
. Góc giữa đường thẳng AD và BC bằng 60...
Đọc tiếp
Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
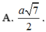
![]()
![]()
Cho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông.
Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có các cạnh
A
D
B
C
3
,
A
C
B
D
4
;
A
B
C
D
2
3
.
Thể tích tứ diện ABCD bằng: A.
2740
12
B.
2047
12
C.
2074...
Đọc tiếp
Cho tứ diện ABCD có các cạnh A D = B C = 3 , A C = B D = 4 ; A B = C D = 2 3 . Thể tích tứ diện ABCD bằng:
A. 2740 12
B. 2047 12
C. 2074 12
D. 2470 12
Cho tứ diện ABCD có
A
B
a
2
,
A
C
A
D
a
,
B
C
B
D
a
,
C
D
a
. Tính thể tích V của khối tứ diện ABCD. A.
V
a
3
2...
Đọc tiếp
Cho tứ diện ABCD có A B = a 2 , A C = A D = a , B C = B D = a , C D = a . Tính thể tích V của khối tứ diện ABCD.
A. V = a 3 2 12
B. V = a 3 6 8
C. V = a 3 6 24
D. V = a 3 2 4
Chọn A
Gọi H là hình chiếu vuông góc của A trên (BCD). Khi đó CD vuông góc với mp(ABH).
Thể tích tứ diện ABCD gấp đôi thể tích của tứ diện ABCE, với E là trung điểm CD.
Cách khác: Gọi I là trung điểm AB.
Dễ thấy IACD và IBCD là các tứ diện vuông tại I, có các cạnh góc vuông là a 2
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
a
2
, ACADa, BCBDa, CDa. Tính thể tích V của khối tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD có A B = a 2 , AC=AD=a, BC=BD=a, CD=a. Tính thể tích V của khối tứ diện ABCD.
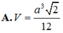
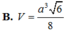
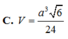
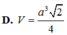
Cho tứ giác ABCD có AM = MN = ND; PB = PQ = QC. Hãy chứng tỏ diện tích tứ giác MNQP = 1/3 diện tích tứ giác ABCD
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).