Cho a; b; c theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?
A. 2b2, a, c2.
B. -2b; -2a; -2c.
C. 2b; a; c.
D. 2b; -a; -c.
Cho a; b; c theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?
A. 2b2, a, c2.
B. -2b; -2a; -2c.
C. 2b; a; c.
D. 2b; -a; -c.
Chọn B.
Ta có a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi a + c = 2b
Suy ra -2( b + c) = -2.2a hay -2b + (-2c) = 2.(-2a)
-2a; -2b; -2c lập thành một cấp số cộng.
Ba số nguyên dương lập thành một cấp số cộng khi một số bất kì bằng trung bình cộng của hai số còn lại. Hãy viết 1 chương trình kiểm tra ba số a,b,c có lập thành cấp số cộng không? GIÚP CỢI Ạ <3
#include <bits/stdc++.h>
using namespace std;
long long a,b,c;
bool kt;
int main()
{
cin>>a>>b>>c;
kt=false;
if (a==(b+c)/2) kt=true;
if (b==(a+c)/2) kt=true;
if (c==(b+a)/2) kt=true;
if (kt==false) cout<<"Khong lap duoc";
else cout<<"Lap duoc";
return 0;
}
Biết rằng ba số x, y, z lập thành một cấp số nhân và ba số x, 2y, 3z lập thành một cấp số cộng. Tìm công bội của cấp số nhân.
Gọi công bội của CSN x ; y ; z là q.
⇒ y = x.q ; z = x.q2.
Lại có : x ; 2y ; 3z lập thành CSC
⇔ 2y – x = 3z – 2y
⇔ 2.xq – x = 3.xq2 – 2.xq
⇔ x(2q – 1) = x.(3q2 – 2q)
⇔ x.(3q2 – 4q + 1) = 0
+ Nếu x = 0 ⇒ y = z = 0
⇒ q không xác định.
+ Nếu x ≠ 0 ⇒ 3q2 – 4q + 1 = 0 ⇔ q = 1 hoặc 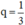
Vậy CSN có công bội q = 1 hoặc 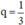
Cho ba số thực a, b, c khác 0. Xét các phát biểu sau
(1) Nếu a, b, c theo thứ tự đó lập thành cấp số cộng
(công sai khác 0) thì ba số 1 a , 1 b , 1 c theo thứ tự đó
cũng lập thành cấp số cộng
(2) Nếu a, b, c theo thứ tự đó lập thành cấp số nhân
thì ba số 1 a , 1 b , 1 c theo thứ tự đó cũng lập thành cấp
số nhân.
Khẳng định nào sau đây là đúng ?
A. (1) đúng, (2) sai
B. cả (1) và (2) đúng
C. cả (1) và (2) sai
D. (2) đúng, (1) sai
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
Tìm ba số, biết theo thứ tự đó chúng lập thành cấp số cộng và có tổng bằng 21, và nếu lần lượt cộng thêm các số 2;3;9 vào ba số đó thì được ba số lập thành một cấp số nhân.
Gọi 3 số cần tìm lần lượt là: \({u_{n - 1}},\;{u_n},\;{u_{n + 1}}\)
Theo tính chất của cấp số cộng ta có: \({u_{n - 1}} + {u_{n + 1}} = 2{u_n}\)
Mà đề bài: \({u_{n - 1}} + {u_n} + {u_{n + 1}} = 21\) suy ra \(3{u_n} = 21\;\)
\(\begin{array}{l} \Leftrightarrow {u_n} = 7\\ \Leftrightarrow \left\{ \begin{array}{l}{u_{n - 1}} = {u_n} - d = 7 - d\\{u_{n + 1}} = {u_n} + d = 7 + d\end{array} \right.\end{array}\)
Lần lượt cộng thêm các số 2, 3, 9 vào 3 số ta được: \({u_{n - 1}} + 2,\;{u_n} + 3,\;{u_{n + 1}} + 9\) hay \(9 - d,\;10,\;16 + d\)
Theo tính chất của cấp số nhân ta có:
\(\begin{array}{l}\left( {9 - d} \right)\left( {16 + d} \right) = {10^2}\\ \Leftrightarrow {d^2} + 7d - 44 = 0\\ \Leftrightarrow \left[ \begin{array}{l}d = - 11\\d = 4\end{array} \right.\end{array}\)
Vậy 3 số cần tìm là: 18; 7; -4 hoặc 3; 7; 11.
Các số a,b,c (theo thứ tự đó) lập thành một cấp số nhân có tổng bằng 26. Tìm các số đó biết rằng: nếu một cấp số cộng có a là số hạng thứ nhất, b là số hạng thứ ba thì c là số hạng thứ chín
Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
Cho ba số a b c , theo thứ tự vừa lập thành cấp số cộng, vừa lập thành cấp số nhân khi và chỉ khi
A. a=d,b=2d,c=3d với d ≢ 0 cho trước
B. a=1,b=2,c=3
C. a=q,b= q 2 ,c= q 3 với q ≢ 0
D. a=b=c
Biết rằng 3 số x, y, z lập thành một cấp số nhân và ba số x, 2y, 3z lập thành một cấp số cộng. Tìm công bội của cấp số nhân ?
Ba số x, y, z lập thành một cấp số nhân nên:
y = x.q và z = y.q = x.q2 ( q là công bội)
Ba số x, 2y, 3z lậo thành một cấp số cộng nên:
x + 3z = 4y ⇔ x + 3.(xq2) = 4.(x.q)
⇔ x. (1 + 3q2 – 4q) = 0 ⇔ x = 0 hay 3q2 – 4q + 1 = 0
Nếu x = 0 thì x = y= z= 0, q là một số tùy ý
Nếu x ≠ 0 thì 3q2– 4q + 1 = 0 ⇔\(\Leftrightarrow\left[{}\begin{matrix}q=1\\q=\dfrac{1}{3}\end{matrix}\right.\).
Công bội của cấp số nhân là \(q=1\) hoặc \(q=\dfrac{1}{3}\).
Chứng minh rằng nếu các số a 2 , b 2 , c 2 lập thành một cấp số cộng a , b , c ≠ 0 thì các số 1 / b + c , 1 / c + a , 1 / a + b cũng lập thành một cấp số cộng.