mọi người làm hộ em 2 câu này với em đang cần ạ.
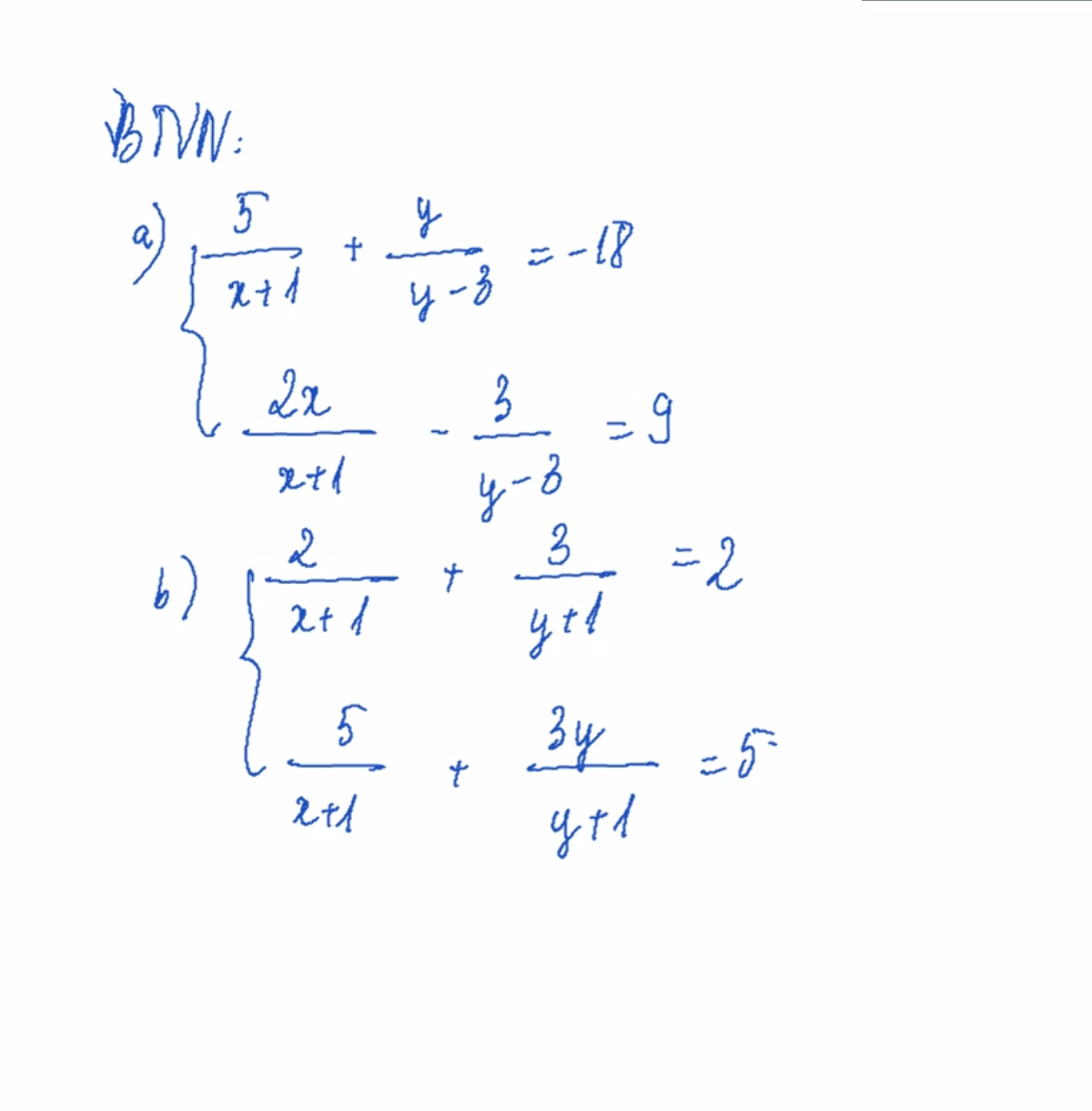
mọi người ai giải hộ em câu này với em đang cần gấp câu này em cảm ơn ạ!

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

MỌI NGƯỜI RÚT GỌN HỘ EM 2 CÂU NÀY Ạ. EM ĐANG CẦN GẤP Ạ . EM CẢM ƠN MỌI NGƯỜI Ạ.
\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
bạn bổ sung đk hộ mình ý 2 là : \(x\ge0;x\ne1\)nhé
cho mk hỏi bạn là nam hay nữ và bạn 2k mấy ạ
Mọi người giải hộ em bài này với ạ, em đang cần gấp ạ
giải thích hộ em câu này với ạ
" người làm vườn tài ba ' nghĩa thông thường và nghĩa theo dụng ý của tác giả với ạ em đang cần gấp ạ
Bạn ko đưa ngữ liệu, đưa ngang như v ai hiểu gì đâu
Bạn học sách mới mà.
mọi người ai làm gấp hộ em câu này với em cảm ơn ạ!
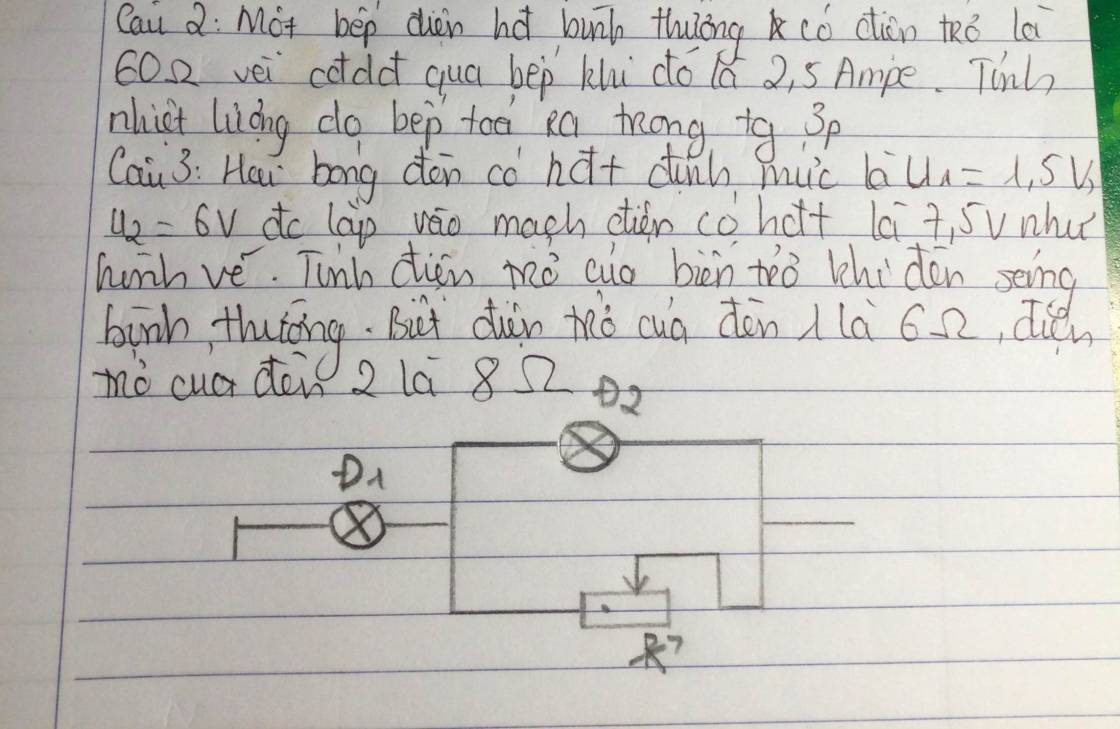
Mọi người ơi giúp em 2 câu này với ạ. Em đang cần gấp ạa🥲
Câu 2.
Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:
\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)
Câu 3.
\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)
\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)
\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)
\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)
CỨU EM CÂU NÀY VỚI Ạ. EM ĐANG CẦN GẤP.
EM CẢM ƠN MỌI NGƯỜI NHIỀU Ạ.

mọi người làm giúp em câu c với ạ
em đang cần gấp ạ
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
em đang cần gấp câu này lắm ạ mọi người giúp em với. em cảm ơn!
Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị