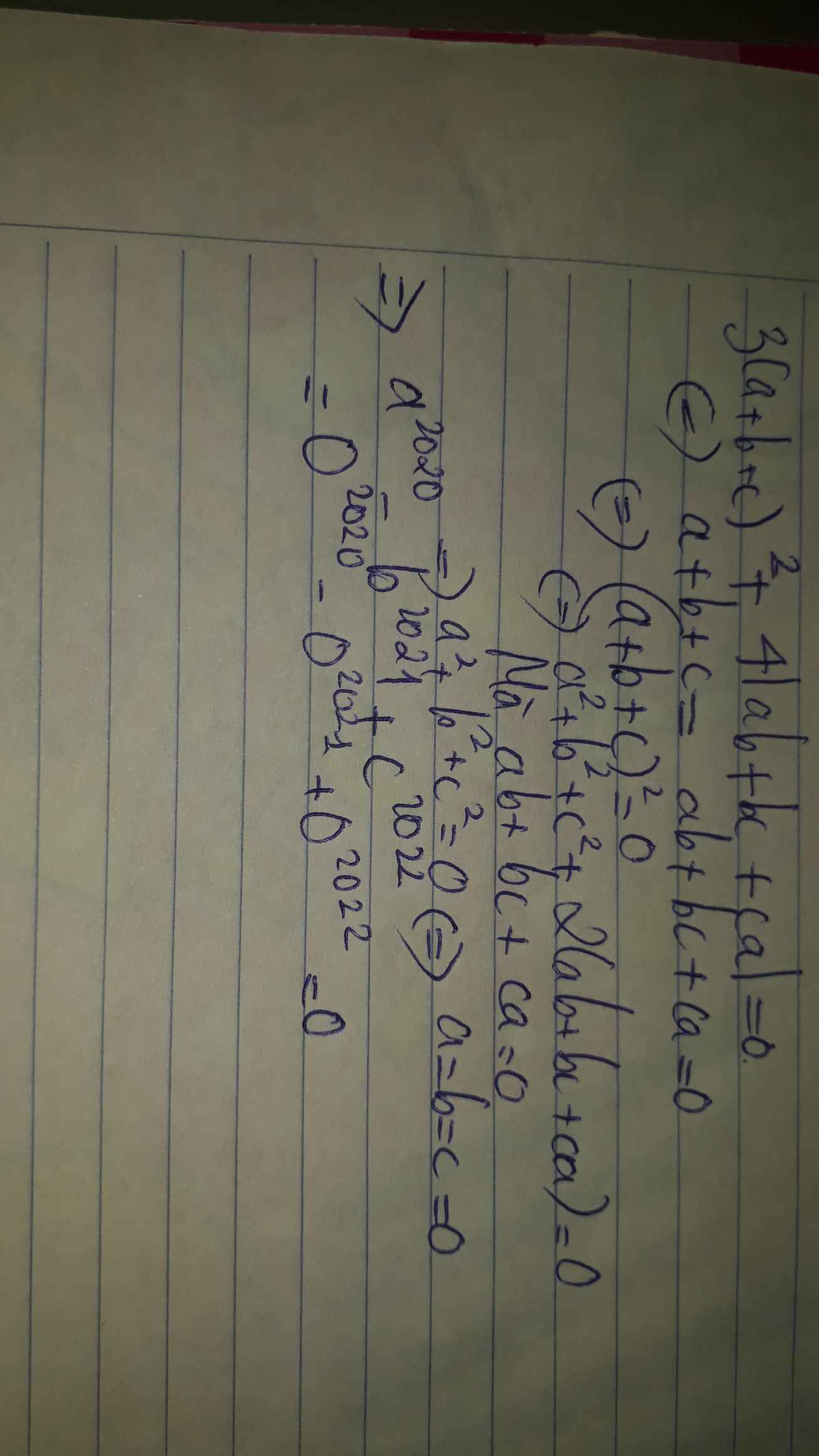Cho a,b,c > 0 và b^2= ac, c^2= ab. Tính B= a^4043/ b^2021 . c^2022
NL
Những câu hỏi liên quan
Cho a,b,c thõa mãn : a^2 + b^2 +c^2 - ab -bc- ca = 0. Tính: P = (a-b)^2020 + (b-c)^2021 + (c-a)^2022
\(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\) (1)
Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\)
Nên PT (1) \(\Leftrightarrow\left\{{}\begin{matrix}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(a-c\right)^2=0\end{matrix}\right.\)
=> a = b = c
\(P=\left(a-b\right)^{2020}+\left(b-c\right)^{2021}+\left(c-a\right)^{2022}\)
\(=\left(a-a\right)^{2020}+\left(b-b\right)^{2021}+\left(c-c\right)^{2022}\)
= 0
Đúng 4
Bình luận (0)
Cho 3(a + b + c)^2 + 4 |ab + bc + ca| = 0. Tính : a^2020 – b^2021 + c^2022. Nhanh lên mn chiều nay mik học rồi
Ta có: \(3\left(a+b+c\right)^2\ge0\forall a,b,c\)
\(4\left|ab+bc+ca\right|\ge0\forall a,b,c\)
Do đó: \(3\left(a+b+c\right)^2+4\left|ab+bc+ca\right|\ge0\forall a,b,c\)
Dấu '=' xảy ra khi a=b=c=0
Ta có: \(a^{2020}-b^{2021}+c^{2022}\)
\(=0^{2020}-0^{2021}+0^{2022}\)
=0
Đúng 1
Bình luận (0)
2.Cho a, b, c là các số thực khác 0 thỏa a ^ 2 + b ^ 2 + c ^ 2 = ab + bc + ca . Tính giá trị của biểu thúc T = (a ^ 2022 + b ^ 2022 + c ^ 2022)/((a + b + c) ^ 2022)
a^2+b^2+c^2=ab+bc+ac
=>2a^2+2b^2+2c^2-2ab-2bc-2ac=0
=>a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2=0
=>(a-b)^2+(b-c)^2+(a-c)^2=0
=>a=b=c
\(T=\dfrac{a^{2022}+a^{2022}+a^{2022}}{\left(3a\right)^{2022}}=\dfrac{3}{3^{2022}}=\dfrac{1}{3^{2021}}\)
Đúng 3
Bình luận (0)
cho a,b,c là cá số thực thoả mãn
a+b+c=2022 và\(\dfrac{1}{a}\)+\(\dfrac{1}{b}\)+\(\dfrac{1}{c}\)=\(\dfrac{1}{2022}\)
tính giá trị của biểu thức B=\(\dfrac{1}{a^{2021}}\)+\(\dfrac{1}{b^{2021}}\)+\(\dfrac{1}{c^{2021}}\)
-Mình làm tắt được không bạn :/?
Đúng 0
Bình luận (2)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}\)
\(\Rightarrow\dfrac{bc+ca+ab}{abc}=\dfrac{1}{a+b+c}\)
\(\Rightarrow\left(bc+ca+ab\right)\left(a+b+c\right)=abc\)
\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc=abc\)
\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+2abc=0\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Rightarrow a=-b\) hay \(b=-c\) hay \(c=-a\)
\(\Rightarrow c=2022\) hay \(a=2022\) hay \(b=2022\)
-Nếu \(a=-b\)\(\Rightarrow B=\dfrac{1}{a^{2021}}+\dfrac{1}{b^{2021}}+\dfrac{1}{c^{2021}}=\dfrac{1}{a^{2021}}-\dfrac{1}{a^{2021}}+\dfrac{1}{2022^{2021}}=\dfrac{1}{2022^{2021}}\)
-Tương tự các trường hợp còn lại.
Đúng 1
Bình luận (0)
Cho a,b>0: \(a^{2019}+b^{2019}=a^{2020}+b^{2020}=a^{2021}+b^{2021}\)
Tính \(P=2022-\left(a+b-ab\right)^{2022}\)
\(a^{2019}+b^{2019}=a^{2020}+b^{2020}\\ \Leftrightarrow a^{2020}-a^{2019}=b^{2019}-b^{2020}=0\\ \Leftrightarrow a^{2019}\left(a-1\right)=b^{2019}\left(1-b\right)\\ \Leftrightarrow\dfrac{a^{2019}}{b^{2019}}=\dfrac{1-b}{a-1}\left(1\right)\\ a^{2020}+b^{2020}=a^{2021}+b^{2021}\\ \Leftrightarrow a^{2021}-a^{2020}=b^{2020}-b^{2021}\\ \Leftrightarrow a^{2020}\left(a-1\right)=b^{2020}\left(1-b\right)\\ \Leftrightarrow\dfrac{a^{2020}}{b^{2020}}=\dfrac{1-b}{a-1}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\dfrac{a^{2019}}{b^{2019}}=\dfrac{a^{2020}}{b^{2020}}\Leftrightarrow\dfrac{a}{b}=1\Leftrightarrow a=b\\ \Leftrightarrow2a^{2019}=2a^{2020}\\ \Leftrightarrow a=1=b\\ \Leftrightarrow P=2022-\left(1+1-1\right)^{2022}=2021\)
Đúng 2
Bình luận (4)
Cho ba số a,b,c thỏa mãn a^2+b^2+c^227 và a+b+c9.
Tính giá trị của biểu thức: (a-4)^2021+(b-4)^2022+(c-4)^2023
có lời giải giúp mình với
Đọc tiếp
Cho ba số a,b,c thỏa mãn a^2+b^2+c^2=27 và a+b+c=9.
Tính giá trị của biểu thức: (a-4)^2021+(b-4)^2022+(c-4)^2023
có lời giải giúp mình với
Lời giải:
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{9^2-27}{2}=27$
$\Rightarrow a^2+b^2+c^2=ab+bc+ac$
$\Leftrightarrow 2(a^2+b^2+c^2)=2(ab+bc+ac)$
$\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
Vì $(a-b)^2; (b-c)^2; (c-a)^2\geq 0$ với mọi $a,b,c$ nên để tổng của chúng bằng $0$ thì $(a-b)^2=(b-c)^2=(c-a)^2=0$
$\Rightarrow a=b=c$
Mà $a+b+c=9$ nên $a=b=c=3$.
Khi đó:
$(a-4)^{2021}+(b-4)^{2022}+(c-4)^{2023}=(-1)^{2021}+(-1)^{2022}+(-1)^{2023}$
$=(-1)+1+(-1)=-1$
Đúng 0
Bình luận (0)
Bài 2. Tính giá trị của biểu thức sau với a =1;b = 0
a) C = (2022 x a + 2022 x b) −2021 x b
b) D = (999 x a −99 x b) + 201 x (a −b)
a/Thay a = 1; b = 0 vào biểu thức C, ta có:
\(C=\left(2022\times1+2022\times0\right)-2021\times0\)
\(=\left(2022+0\right)-0\)
\(=2022\)
b/Thay a = 1; b = 0 vào biểu thức D, ta có:
\(D=\left(999\times1-99\times0\right)+201\times\left(1-0\right)\)
\(=\left(999-0\right)+201\times1\)
\(=999+201\)
\(=1200\)
#deathnote
Đúng 3
Bình luận (0)
cho 3 số a,b,c thoả mãn \(\dfrac{a}{2020}=\dfrac{b}{2021}=\dfrac{c}{2022}\)
Chứng minh rằng (a-c)3+8(a-b)2.(c-b)=0
Bài này xuất hiện trong câu cuối đề GKI năm ngoái của mình :v
-Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{2020}=\dfrac{c}{2022}=\dfrac{a-c}{2020-2022}=\dfrac{a-c}{-2}\\\dfrac{a}{2020}=\dfrac{b}{2021}=\dfrac{a-b}{2020-2021}=\dfrac{a-b}{-1}\\\dfrac{c}{2022}=\dfrac{b}{2021}=\dfrac{c-b}{2022-2021}=c-b\end{matrix}\right.\)
\(\Rightarrow c-b=-\left(a-b\right)=\dfrac{a-c}{-2}\)
\(\Rightarrow\left\{{}\begin{matrix}a-c=-2\left(c-b\right)\\a-b=-\left(c-b\right)\end{matrix}\right.\)
\(\left(a-c\right)^3+8\left(a-b\right)^2.\left(c-b\right)=\left[-2\left(c-b\right)\right]^3+8\left[-\left(c-b\right)\right]^2.\left(c-b\right)=-8\left(c-b\right)^3+8\left(c-b\right)^3=0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cho các số thực a, b thỏa mãn: a^3 - 3a^2 + 5a - 2022=0 và b^3 -3b^2+5b+2016=0. Tính S=(a+b-1)^2021+(a+b-3)^2022