mn giúp mình bài này đi

Mn ơi giải giúp mình bài hình này nhé khoảng tầm 22h mình quay lại lấy nha mai đi học r mình đang cần gấp cảm ơn mn 
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
x^2-6x+8=0
Mn giúp mình giải bài này thành nhiều cách đi mình đang cần gấp
Mình biết làm 1 cách thui, mong bạn thông cảm nha!
\(x^2-6x+8=0\Leftrightarrow x^2-2x-4x+8=0\)
\(\Leftrightarrow x\left(x-2\right)-4\left(x-2\right)=0\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-2=0\\x-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\x=4\end{cases}}}\)
Chúc may mắn nha!
Mn ơi cho mình hỏi bài này làm sao vậy
Bài này thuộc dạng làm tròn số
Đề Bài: 2x=3y=5z và x-y=z = -33
Mn giải giúp mình nhé vì bài này mà mình bị đau đầu mấy ngày liền![]()
![]()
bạn ơi cái này là tìm về cái gì?
ý bạn là \(x-y-z=-33?\)
Ta có \(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y-z}{15-10-6}=\dfrac{-33}{-1}=33\\ \Rightarrow\left\{{}\begin{matrix}x=33\cdot15=495\\y=33\cdot10=330\\z=33\cdot6=198\end{matrix}\right.\)
Mn giúp tớ bài này vì mình cần rất gấp ạ. Mong mn giúp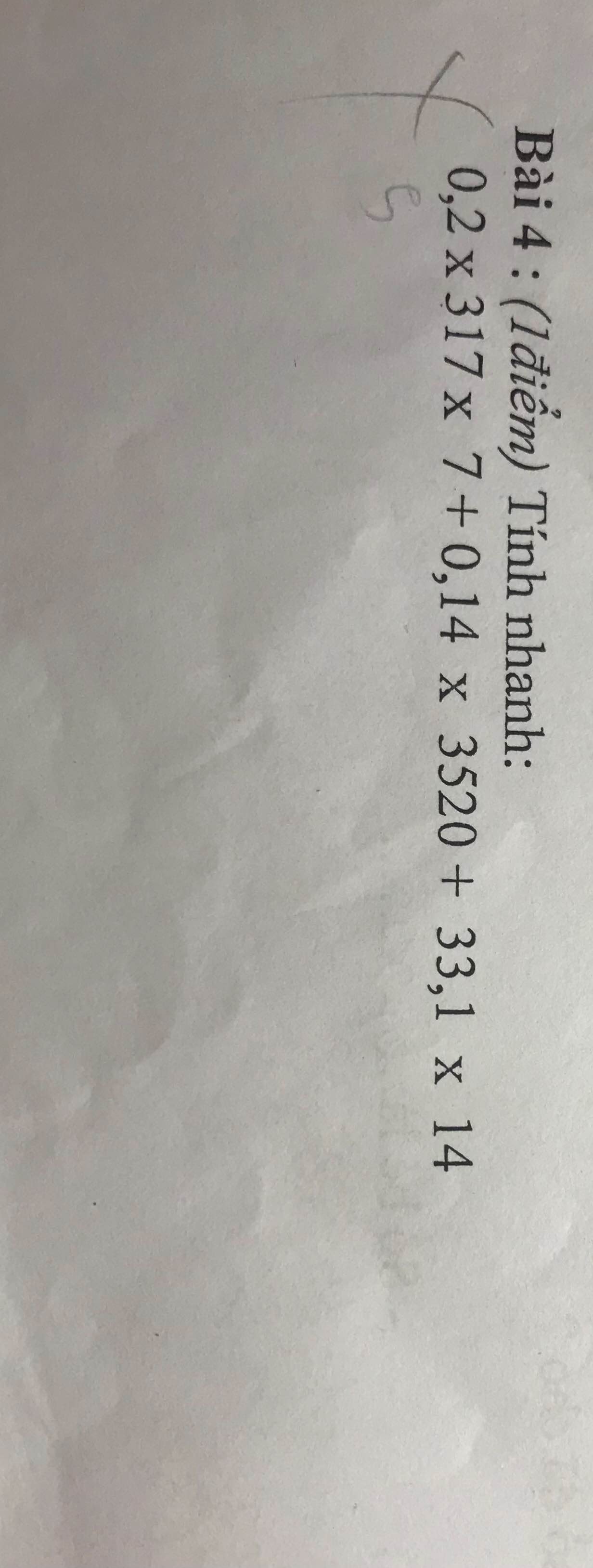
Mn giải giúp mình đề này với, ai làm được bài nào thì giúp mình luôn nhé. cám ơn mn
Giúp giúp mình bài này với mn ơi

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)
Mn giúp mình bài này với nha, cảm ơn mn 
\(Ba\left(NO_3\right)_2+H_2SO_4\rightarrow2HNO_3+BaSO_4\downarrow\)
\(CaCO_3+HNO_3\rightarrow Ca\left(NO_3\right)_2+CO_2\uparrow+H_2O\)
\(3AgNO_3+H_3PO_4\rightarrow AgPO_4\downarrow+HNO_3\)
Anh thấy PTHH đầu 2 chất kết tủa không hợp lí nhá. Em coi lại đề có phải 1 kết tủa 1 bay hơi không nha
mn giúp mình bài này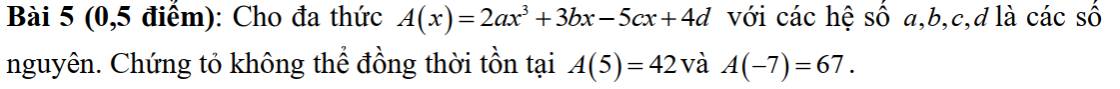
mn giúp mình bài này với