Cho tam giác ABC là tam giác đều, có AB= 5cm, tính độ dài đường cao BH
H24
Những câu hỏi liên quan
a) Cho tam giác ABC vuông tại A, đường cao AH = 2cm. Tính các cạnh của tam giác ABC biết: BH = 1cm, HC = 3cm.
b) Cho tam giác ABC đều có AB = 5cm. Tính độ dài đường cao BH?
b: \(BH=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
a: Đề sai rồi bạn
Đúng 1
Bình luận (0)
a.=> BC = BH + CH = 1 + 3 = 4 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=HB^2+AH^2\)
\(AB=\sqrt{1^2+2^2}=\sqrt{5}cm\)
áp dụng định lí pitago vào tam giác vuông AHC
\(AC^2=AH^2+HC^2\)
\(AC=\sqrt{2^2+3^2}=\sqrt{13}cm\)
Đúng 1
Bình luận (0)
a) Cho tam giác ABC vuông tại A, đường cao AH = 2cm. Tính các cạnh của tam giác ABC
biết: BH = 1cm, HC = 3cm.
b) Cho tam giác ABC đều có AB = 5cm. Tính độ dài đường cao BH?
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AB=\sqrt{BH^2+AH^2}=\sqrt{5}cm\)
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4+9}=\sqrt{13}\)cm
-> BC = HB + HC = 4 cm
b, Ta có tam giacs ABC đều mà BH là đường cao hay BH đồng thời là đường trung tuyến
=> AH = AC/2 = 5/2
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=\dfrac{5\sqrt{3}}{2}cm\)
Đúng 5
Bình luận (0)
Cho tam giác ABC đều có AB= 5cm. Tính đường cao BH (BH vuông góc với AC tại H)
Vì tam giác ABC đều => AB = AC = BC = 5cm
Xét tam giác ABC đều có BH là đường cao => BH đồng thời là đường trung tuyến
=> H là trung điểm AC => AH = 1/2 AC = 1/2 . 5 = 2,5 (cm)
Xét tam giác ABH vuông tại H có: \(AH^2+BH^2=AB^2\)(định lý Pytago)
=> \(2,5^2+BH^2=5^2\)
<=> 6,25 + BH^2 = 25
<=> BH^2 = 18,75
Vì BH > 0 => BH = \(\sqrt{18,75}\approx4,33\)
Vậy BH \(\approx4,33\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=AC=5cm BC=6cm đường cao AH xuất phát từ đỉnh A của tam giác ABC (H thuộc BC) a)chứng minh tam giác AHB =AHC b)chứng minh AH là tia phân giác của góc A c)tính độ dài các đoạn thẳng BH và AH
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
c: BH=CH=3cm
AH=căn 5^2-3^2=4cm
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại B, kẻ CH vuông góc AB. Biết AH= 1cm, BH= 4cm. Tính độ dài AC.
Bài 2: Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
Bài 3: Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=BC.
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Đúng 0
Bình luận (0)
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
Đúng 0
Bình luận (0)
C1 Cho tam giác vuông ABC vuông tại A, đường cao AH , biết AB9cm,AC12cm, tính độ dài cạnh AH
C2 Cho tam giác ABC vuông tại A, đường cao AH, biết BH5cm,HC6cm. Tính độ dài cạnh AB
C3 Đồ thị hai hàm số y3x + 2 và y (2m+1)x+k-1 là 2 đường thẳng cắt nhau tại 1 điểm trên trục tung khi ( giải hẳn ra)
C4 Trong các hàm số y 3 - 2x ,y √3(x+1)-5;y1/2x+6;y-1,5x hàm số không phải hàm số bậc nhất là (giải hẳn ra)
Giúp mình với
Đọc tiếp
C1 Cho tam giác vuông ABC vuông tại A, đường cao AH , biết AB=9cm,AC=12cm, tính độ dài cạnh AH
C2 Cho tam giác ABC vuông tại A, đường cao AH, biết BH=5cm,HC=6cm. Tính độ dài cạnh AB
C3 Đồ thị hai hàm số y=3x + 2 và y= (2m+1)x+k-1 là 2 đường thẳng cắt nhau tại 1 điểm trên trục tung khi ( giải hẳn ra)
C4 Trong các hàm số y = 3 - 2x ,y =√3(x+1)-5;y=1/2x+6;y=-1,5x hàm số không phải hàm số bậc nhất là (giải hẳn ra)
Giúp mình với
Câu 1:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{9^2}+\dfrac{1}{12^2}=\dfrac{1}{81}+\dfrac{1}{144}=\dfrac{25}{1296}\)
\(\Leftrightarrow AH^2=\dfrac{1296}{25}\)
hay \(AH=\dfrac{14}{5}=4.8cm\)
Vậy: AH=4,8cm
Câu 2:
Ta có: BC=BH+CH(H nằm giữa B và C)
hay BC=5+6=11(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=5\cdot11=55\)
hay \(AB=\sqrt{55}cm\)
Vậy: \(AB=\sqrt{55}cm\)
Câu 4:
Không có hàm số nào không phải là hàm số bậc nhất
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = 5cm, AC = 12cm và BC = 13cm . Kẻ đường cao AH (H ∈ BC) . Tính độ dài các đoạn thẳng BH và CH.
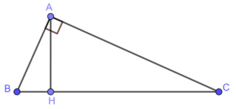
Ta có: A B 2 + A C 2 = 5 2 + 12 2 = 25 + 144 = 169 = 13 2 = B C 2
Suy ra, tam giác ABC vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
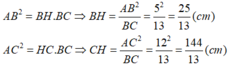
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC có 3 cạnh AB, AC,BC lần lượt là 2cm ; 3cm ; 4cm. Kẻ đường cao AH : Tính :a, Độ dài các đoạn thẳng BH, HC, AHb, Độ dài đường cao tương ứng với cạnh AB , ACc, Số đo các góc A, B, C của tam giác ABC ( làm tròn đến phút )Bài 2 : Cho tam giác ABC có góc A 45 độ , góc B 30 độ và AB 5cm . Kẻ đường cao AH . Tính :a,Độ dài các đoạn thẳng AH, BH, HCb, Tính diện tích tam giác ABC ) làm tròn kết quả đến hàng % )Bài 3 : Cho tam giác ABC vuông tại A . Đường cao AH 6cm ; frac{HB}{H...
Đọc tiếp
Bài 1 : Cho tam giác ABC có 3 cạnh AB, AC,BC lần lượt là 2cm ; 3cm ; 4cm. Kẻ đường cao AH : Tính :
a, Độ dài các đoạn thẳng BH, HC, AH
b, Độ dài đường cao tương ứng với cạnh AB , AC
c, Số đo các góc A, B, C của tam giác ABC ( làm tròn đến phút )
Bài 2 : Cho tam giác ABC có góc A = 45 độ , góc B = 30 độ và AB = 5cm . Kẻ đường cao AH . Tính :
a,Độ dài các đoạn thẳng AH, BH, HC
b, Tính diện tích tam giác ABC ) làm tròn kết quả đến hàng % )
Bài 3 : Cho tam giác ABC vuông tại A . Đường cao AH = 6cm ; \(\frac{HB}{HC}=\frac{4}{9}\) ;tính các cạnh của tam giác ABC
Mọi người giúp em giải 3 bài này với
thứ 6 em kiểm tra rồi
mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)
Đúng 1
Bình luận (0)
a,Cho tam giác ABC vuông tại A,đường cao AH=2cm.Tính các cạnh của tam giác ABC biết:BH=1cm,HC=3cm
b,Cho tam giác ABC đều có AB=5cm.Tính độ dài đường cao BH ?
a) Xét tam giác ABH vuông tại H. Áp dụng định lý Pi-ta-go trong tam giác vuông ta có:
BH2+AH2=AB2
<=> 1+4=5(cm)
<=> AB=\(\sqrt{5}\)cm
Xét tam giác AHC vuông tại H. Áp dụng định lí Pi-ta-go ta có:
HC2+AH2=AC2
<=> 9+4=13(cm)
<=> AC=\(\sqrt{13}\left(cm\right)\)
Xét BC=BH+HC=1+3=4(cm)
b) Áp dụng công thức tính đường cao trong tam giác đều, ta có:
BH=\(5\cdot\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}\)




