tim x,y
3xy -6x +y+3 =0
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
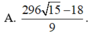
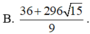
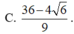
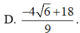
tìm x; y
3xy-x+y=5
\(x\left(3y-1\right)+y=5\)
\(3x\left(3y-1\right)+3y=15\)
\(3x\left(3y-1\right)+3y-1=14\)
\(\left(3x-1\right)\left(3y-1\right)=14\)
Đến đây đưa về phương trình ước số
3xy-x+y=5
Ta tính:3xy-x+y=5
Ta có :
\(3\times x-x+y-x+y=5\) (ta chuyển xy thành x-y)
\(\Rightarrow3-1x=5\)
x =3-5
x=-2
Vậy x=-2
Ta tính:\(3\times-2y=5\)
Sau khi ta có x=-2 thì:
\(-2y=3-5\)
\(-2y=-2\)
\(y=-2\div-2\)
\(y=1\)
Vậy y=1
Suy ra x=-2 và y=1
tim x,y:
3xy-6x+y+3=0
3xy - 6x + y + 3 = 0
=> 3x.(y - 2) + y - 2 + 5 = 0
=> (y - 2).(3x + 1) = -5
Ta có bảng sau:
| 3x+1 | -5 | -1 | 1 | 5 |
| x | -2 | -2/3 | 0 | 4/3 |
| y-2 | 1 | 5 | -5 | -1 |
| y | 3 | 7 | -3 | 1 |
Vậy...
*Thiếu điều kiện x,y thuộc ...? , bổ sung rồi loại bớt.
Tim x , y , z biet : x^2 +y^2 -2z+4y +5=0
Tim GTLN cua bieu thuc P = -x^2 +6x +1
\(P=-x^2+6x+1=-\left(x^2-6x+9\right)+10=-\left(x-3\right)^2+10\le10\)Vậy \(Max_P=10\) khi \(x-3=0\Rightarrow x=3\)
b, \(P=-x^2+6x+1=-\left(x^2-6x-1\right)\)
\(=-\left(x^2-3x-3x+9-10\right)\)
\(=-\left[\left(x-3\right)^2-10\right]\)
Với mọi giá trị của \(x\in R\) ta có:
\(\left(x-3\right)^2\ge0\Rightarrow\left(x-3\right)^2-10\ge-10\)
\(\Rightarrow-\left[\left(x-3\right)^2-10\right]\ge10\)
Hay \(P\ge10\) với mọi giá trị của \(x\in R\).
Để \(P=10\) thì \(-\left[\left(x-3\right)^2-10\right]=10\)
\(\Rightarrow\left(x-3\right)^2=0\Rightarrow x=3\)
Vậy.....
Chúc bạn học tốt!!!
1 tim x
2x^4-6x^3+x^2+6x-3=0
2x4 - 6x3 + x2 + 6x - 3 = 0
=> 2x4 - 2x3 - 4x3 + 4x2 - 3x2 + 3x + 3x - 3 = 0
=> 2x3(x - 1) - 4x2(x - 1) - 3x(x - 1) + 3(x - 1) = 0
=> (x - 1)(2x3 - 4x2 - 3x + 3) = 0
=> (x - 1)(2x3 + 2x2 - 6x2 - 6x + 3x + 3) = 0
=> (x - 1)[2x2(x + 1) - 6x(x + 1) + 3(x + 1)] = 0
=> (x - 1)(x + 1)(2x2 - 6x + 3) = 0
\(\Rightarrow\left[{}\begin{matrix}x-1\\x+1\\2x^2-6x+3\end{matrix}\right.\) (2x2 - 6x + 3 vô nghiệm)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
1. phan tich da thuc thanh nhan tu
a. x^2+3x-5 b. 4x^2-16x+7 c. 5x^2-6x-7 d.x^4+2x^3-4x-4
2. tim x,y bt: x^2+y^2+z^2=xy+yz+zx va x^2012+y^2012+z^2012= 3^2013
3. tim x: a. x^2-4x=21 b. x^2-4x+4=0 c.x^2-6x=2x=11 d. 4^x-12.2^x+32=0
tìm xy nguyen biet (x+y-2)^2+(y+3)^2=0 tim xy thoa man x^2-6x+10=1/|x-3|+1
tim x,y biet 5x^2+6x-4xy-2y+2+y^2=0
\(5x^2+6x-4xy-2y+2+y^2=0\)
\(\Leftrightarrow4x^2+x^2+2x+4x-4xy-2y+1+1+y^2=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+\left(4x-2y\right)+\left(x^2+2x+1\right)+1=0\)
\(\Leftrightarrow\left(2x-y\right)^2+2\left(2x-y\right)+1+\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(2x-y+1\right)^2+\left(x+1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-y+1\right)^2=0\\\left(x+1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y+1=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2.\left(-1\right)-y+1=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2-y+1=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1-y=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=-1\end{matrix}\right.\)
Vậy \(x=-1\) và \(y=-1\)
Tim x,
a,2x^4-6x^3+x^2+6x-3=0
b,x^3-9x^2+26x+24=0
c, P= 2x^4 - 4x^3 + 6x^2 - 4x + 5 biet rang x^2 - x=7
a)\(2x^4-6x^3+x^2+6x-3=0\)
\(\Leftrightarrow2x^4-6x^3+3x^2-2x^2+6x-3=0\)
\(\Leftrightarrow x^2\left(2x^2-6x+3\right)-\left(2x^2-6x+3\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(2x^2-6x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(2x^2-6x+3\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-1=0\\x+1=0\\2x^2-6x+3=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1\\x=-1\\\Delta_{2x^2-6x+3}=\left(-6\right)^2-4\left(2.3\right)=12\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1\\x=-1\\x_{1,2}=\frac{6\pm\sqrt{12}}{4}\end{array}\right.\)
b)\(x^3+9x^2+26x+24=0\)
\(\Leftrightarrow x^3+5x^2+6x+4x^2+20x+24=0\)
\(\Leftrightarrow x\left(x^2+5x+6\right)+4\left(x^2+5x+6\right)=0\)
\(\Leftrightarrow\left(x^2+5x+6\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+2=0\\x+3=0\\x+4=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\\x=-3\\x=-4\end{array}\right.\)