Cho tứ diện ABCD. gọi G₁, G₂ là trọng tâm ∆ABD và ∆ACD. C/m: G₁ G₂ // (ABC) G₁ G₂ // (BCD)
TD
Những câu hỏi liên quan
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm
∆
A
B
C
;
∆
A
B
D
;
∆
A
C
D
;
∆
B
C
D
. Tính thể tích khối tứ diện MNPQ theo V. A.
V
9
B.
V
3
C. ...
Đọc tiếp
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
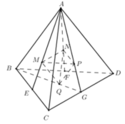
A. V 9
B. V 3
C. 2 V 9
D. V 27
Ta có:
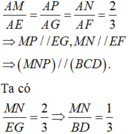
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
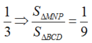
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
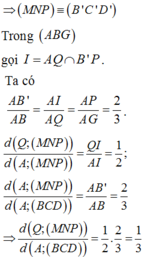

Chọn D.
Đúng 1
Bình luận (0)
cho hình tứ diện ABCD. Gọi M là điểm trên cạnh AD sao cho MA = 2MD
a, G là trọng tâm tam giác ABD. Chứng minh rằng: MG // (BCD)
b, H là trọng tâm tam giác ABC. Chứng minh rằng: HG // (BCD)
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Đúng 1
Bình luận (1)
(Bài này làm như nào vậy mn?)Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; A_1,B_1,C_1,D_1 lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?A. 71/1001B. 75/1001C. 74/1001D.10/143
Đọc tiếp
(Bài này làm như nào vậy mn?)
Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; \(A_1,B_1,C_1,D_1\) lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?
A. 71/1001
B. 75/1001
C. 74/1001
D.10/143
(Bài này làm như nào vậy mn?)Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; A_1,B_1,C_1,D_1 lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?A. 71/1001B. 75/1001C. 74/1001D.10/143
Đọc tiếp
(Bài này làm như nào vậy mn?)
Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; \(A_1,B_1,C_1,D_1\) lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?
A. 71/1001
B. 75/1001
C. 74/1001
D.10/143
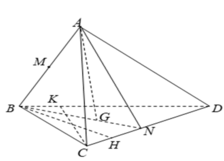
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M thuộc đoạn thẳng BC sao cho BM = 2MC. Giao tuyến của mặt phẳng (BGM) và (ACD)
\(BG\) cắt \(AD\) tại \(K\), \(BM\) cắt \(AC\) tại \(C\).
Giao tuyển của hai mặt phẳng \(\left(BGM\right)\) và \(\left(ACD\right)\) là \(CK\).
Đúng 1
Bình luận (0)
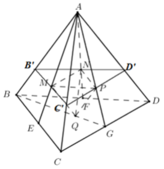
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi
G
1
là giao điểm của AG và mp(BCD),
G
2
là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng? A.
G
1
G
2
/
/
A
B
B.
G
1
G
2
/
/...
Đọc tiếp
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi G 1 là giao điểm của AG và mp(BCD), G 2 là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng?
A. G 1 G 2 / / A B
B. G 1 G 2 / / A C
C. G 1 G 2 / / C D
D. G 1 G 2 / / A D
Đáp án A.
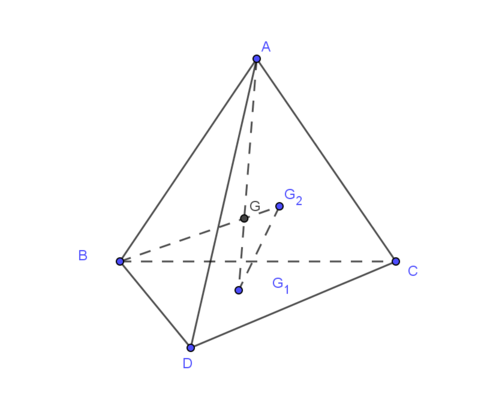
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B
Đúng 0
Bình luận (0)
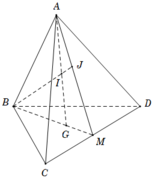
Cho tứ diện ABCD ; gọi G là trọng tâm tam giác BCD và M là trung điểm CD; I là điểm ở trên đoạn thẳng AG; BI cắt (ACD) tại J. Chọn khẳng định sai?
A. giao tuyến của (ACD) và ( ABG) là AM
B. 3 điểm A; J; M thẳng hàng
C. J là trung điểm của AM
D. giao tuyến của (ACD) và ( BDJ) là DJ
Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB và CD. G là trọng tâm của tam giác BCD. Tìm giao điểm của EG với (ACD)
Cho tứ diện ABCD. G là trọng tâm tam giác BCD. Tìm giao tuyến của hai mặt phẳng (ACD) và (GAB).
Đọc tiếp
Cho tứ diện ABCD. G là trọng tâm tam giác BCD. Tìm giao tuyến của hai mặt phẳng (ACD) và (GAB).
![]()
![]()
![]()
![]()