Cho △ ABC vuông tại A. Đường cao AH. CMRa) AB2 = BH.BCb) AH2= HB.HC
MN
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , đường cao AH . CMRa, AB2 BH . BC , AC2 CH.BHb, AH2 AH.BHc, AB.AC AH.BCgải giùm nha mik cần gấp
a) Cm tamgiac ABC đồng dạng với tamgiac HBA(g.g)
=> AB/BC = BH/AB hay AB^2 = BH.HC
và cm tamgiac ABC đồng dạng với tamgiac HAC(g.g)
=> AC/BC = HC/AC hay AC^2 = CH.BH
a. Xét tg vuông ABC và tg vuông HBA có:
\(\widehat{ABH}\)chung
\(\Rightarrow\Delta ABC~\Delta HBA\)
\(\Rightarrow\frac{AB}{HB}=\frac{BC}{BA}\)
\(\Rightarrow AB^2=HB.BC\)
Cmtt:\(\Delta ABC~HAC\)
\(\Rightarrow\frac{AC}{HC}=\frac{BC}{AC}\)
\(\Rightarrow AC^2=BC.HC\)
b. lát làm tiếp nhá
b.Xét tg vuông ABH và tg vuông CAH có:
\(\widehat{ABH}=\widehat{HAC}\)(cùng phụ\(\widehat{BAH}\))
\(\Rightarrow\Delta ABH~\Delta CAH\)
\(\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=CH.BH\)
c.Chịu
Cho tam giác ABC vuông tại A có đường cao AH. Chứng minh: giải câu e thôi mấy câu kia bt làm r
a) AB
2 = BH.BC
b) AH2 = HB.HC
c) AB.AC = AH.BC
d)
2 2 2
1 1 1
AH AB AC
= +
e) Biết AB = 3cm, BC = 5cm. Tính AH?
Theo Pytago tam giác ABC vuông tại A ta có
\(AC=\sqrt{BC^2-AB^2}=4cm\)
Ta có \(S_{ABC}=\dfrac{1}{2}.AH.BC;S_{ABC}=\dfrac{1}{2}.AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH ( H thuộc BC)
a) Chứng minh : tam giác ABH đồng dạng tam giác CBA sau đó suy ra AB2= BH.BC
b) Chứng minh AH2=BH.CH
C) Gọi M là trung điểm của BH, kẻ CK vuông góc với AM tại K, CK cắt AH tại I. Chứng minh IA=IH
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
=>BA/BC=BH/BA
=>BA^2=BH*BC
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
c: Xét ΔCAM có
CK,AH là đường cao
CK cắt AH tại I
=>I là trực tâm
=>MI vuông góc AC
=>MI//AB
Xét ΔHAB có
M là trung điểm của HB
MI//AB
=>I là trung điểm của HA
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác ABC vuông tại A , đường cao AH
a) Cho biết HB=9cm,HC=16cm. Tính các độ dài AH,AB=AC
b) Chứng minh các hệ thức AH2=HB.HC, AB2=BC.BH
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Chứng minh: AH2 = HB.HC.
Xét \(\Delta HBA\) vuông tại \(H,\Delta ABC\) vuông tại \(A:\)
\(\widehat{ABH}:Chung \)
\(\widehat{BAC}=\widehat{BHA}=90^o \)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{HB}=\dfrac{HC}{HA}\)
\(\Rightarrow AH^2=HB.HC\)
Đúng 1
Bình luận (1)
Lời giải:
Xét tam giác $HBA$ và $HAC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ với $\widehat{BAH}$)
$\Rightarrow \triangle HBA\sim \triangle HAC$ (g.g)
$\Rightarrow \frac{HB}{HA}=\frac{HA}{HC}$
$\Rightarrow HA^2=HB.HC$
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh
a) A B 2 = B H . B C ;
b) A H 2 = B H . H C .
a) Chứng minh được
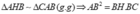
b) HS tự chứng minh
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH. a/ cm AH2= HB.HC. b/biết HB=3,6cm, HC=6,4cm. Tính BC, AH, AB, AC
a: Xet ΔABC vuông tại A co AH là đường cao
nên AH^2=HB*HC
b: BC=3,6+6,4=10cm
\(AH=\sqrt{3.6\cdot6.4}=4.8\left(cm\right)\)
\(AB=\sqrt{3.6\cdot10}=6\left(cm\right)\)
=>AC=8cm
Đúng 0
Bình luận (0)
Cho Tam Giác vuông ABC (góc A=90 độ ) , đường cao AH . Biết BH =4cm , CH=9cm
a) Chứng minh :AB2=BH.BC
b)Tính AB , AC
Bạn tự vẽ hình nhé
a) Xét Tg ABC và Tg HBA có:
Góc BAC = Góc AHB(=90độ)
Góc B chung
=> Tg ABC ~ Tg HBA(g.g)
=> AB/HB=BC/BA
=> AB^2=HB. BC
=> Đpcm
b) BC= BH+ HC= 4+9=13cm
Có AB^2= HB.BC (câu a)
=> AB^2= 4.13= 52
=> AB= căn 52(cm)
Có Tg ABC vuông tại A
=> AC^2= BC^2-AB^2= 13^2- 52=117
=> AC= căn 117 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH ( H ϵ BC)
a) chứng minh : △ABC đồng dạng △HAC và AB. AC= AH.BC
b) chứng minh: AC2 = HC.BC
c) chứng minh : AH2= HB.HC
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot AH\cdot BC\)
=>AB*AC=AH*CB
b: Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=HC*BC
c: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
Đúng 2
Bình luận (0)




