Cho △ABC cân tại A, kẻ AH vuông góc với BC. Chứng minh △ABH=△AHC bằng 2 cách
LL
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A ,AB bằng 9 cm ,AC bằng 12 cm .Kẻ AH vuông góc với BC tại H
a/Chứng minh tam giác abh đồng dạng tam giác ABC và AB mũ 2 = Hb . BC
b/tính BC, ah
c/tia phân giác góc ACB cắt ah tại I và cắt AB tại D Chứng minh CB.CI=CA.CDCD
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
Đúng 0
Bình luận (0)
Cho tam giác cân ABC cân tại A. Kẻ AH vuông góc với BC. Chứng mình rằng tam giác AHB=AHC ( giải bằng hai cách)
theo dề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2
theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )
Đúng 0
Bình luận (0)
C1: Xét tg AHB và tg AHC có:
AH chung
AB=AC( tg ABC cân tại A)
=> tg AHB=tg AHC (cạnh huyền-cạnh góc vuông)
C2: Xét tg AHB và tg AHC có:
AB=AC(tgABC cân tại A)
góc B= góc C (tg ABC cân tại A)
=> tg AHB=tg AHC (cạnh huyền-góc nhọn
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh ∆ A H B = ∆ A H C .
Chứng minh được △ A H B = △ A H C (cạnh huyền - cạnh góc vuông)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a. Kẻ ah v góc với bc. Chứng minh rằng tam giác ahb = tam giác ahc ( giải bằng hai cách)
theo đề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2 theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )
Đúng 0
Bình luận (0)
minh nghi cau tra loi khac voi minh tai sao lai co duong cao minh khong hieu
Đúng 0
Bình luận (1)
Bài 3: (5diểm) Cho tam giác ABC cân tại A, Kẻ AH vuông góc với BC(H € BC)
a) chứng minh ∆ABH=∆ACH
b) chứng minh AH là tia phân giác của góc BAC.
c) ChoAH = 3cm , BC - 8 cm . Tính độ dài AC.
d) Kẻ HE vuông góc với AB, HD vuông góc với AC . Chứng minh tam giác AED là tam giác cân.
a) Xét \(\Delta ABH\) vuông tại H và \(\Delta ACH\text{vuông tại H}:\)
AB = AC \((\Delta ABC\text{cân tại A}).\)
\(\widehat{B}=\widehat{C}\) \((\Delta ABC\text{cân tại A}).\)
\(\Rightarrow\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn).
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao \(\left(AH\perp BC\right).\)
\(\Rightarrow\) AH là phân giác \(\widehat{BAC}.\)
c) Ta có: BH = CH = \(\dfrac{1}{2}BC=\dfrac{1}{2}8=4\left(cm\right).\)
Xét \(\Delta ABH:\)
\(AB^2=AH^2+BH^2\left(Pytago\right).\\ \Rightarrow AB^2=3^2+4^2.\\ \Rightarrow AB=5\left(cm\right).\)
Mà AB = AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow AC=5\left(cm\right).\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC.
a) Chứng minh tam giác ABH = tam giác ACH
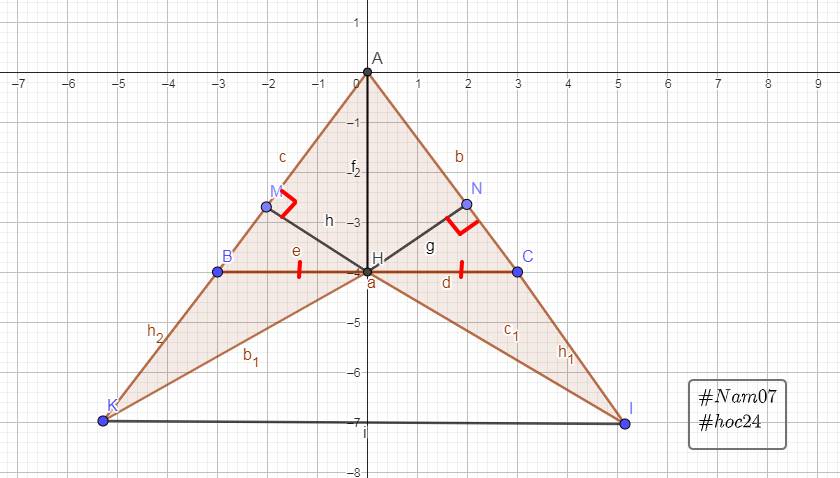
b) Kẻ HM vuông góc với AB, HN vuông góc với AC. Chứng minh tam giác AMN cân.
c) Chứng minh MN // BC
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
Đúng 3
Bình luận (1)
Cho tam giác ABC nhọn, kẻ đường cao AH (H thuộc cạnh BC). Tia phân giác của góc ABH cắt AH tại I. Qua A kẻ đường thẳng vuông góc với AB, cắt tia BI tại K. Kẻ KD vuông góc với BC (D thuộc BC). a) Chứng minh rằng: tam giác AKD cân. b) Chứng minh rằng: BK vuông gióc với AD . Từ đó suy ra I là trực tâm của tam giác ABD. c) Trên tia đối của tia HA lấy điểm E sao cho HE HI. Chứng minh rằng AKDE là hình thang cân. d) Nếu biết rằng ADE 3ADK , tính số đo ABC.
Đọc tiếp
Cho tam giác ABC nhọn, kẻ đường cao AH (H thuộc cạnh BC). Tia phân giác của góc ABH cắt AH tại I. Qua A kẻ đường thẳng vuông góc với AB, cắt tia BI tại K. Kẻ KD vuông góc với BC (D thuộc BC). a) Chứng minh rằng: tam giác AKD cân. b) Chứng minh rằng: BK vuông gióc với AD . Từ đó suy ra I là trực tâm của tam giác ABD. c) Trên tia đối của tia HA lấy điểm E sao cho HE = HI. Chứng minh rằng AKDE là hình thang cân. d) Nếu biết rằng ADE 3ADK , tính số đo ABC.
tam giác ABC cân tại A,H là trung điểm của BC
a.Chứng minh tam giác ABH =tam giác AHC và AH vuông góc với BC
b,kẻ HM vuông góc với AC tại M, kẻ HN vuông góc với AC tại N.Chứng minh tam giác AHM=Tam giác AHN
c. Gọi I là giao điểm của MH và AC,K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
Đúng 1
Bình luận (0)
Cho tam giác cân ABC cân tại A Kẻ AH vuông góc BC Kẻ HI vuông góc AB Kẻ HKC vuông góc AC
a. chứng minh tam giác AHB= tam giác AHC
b. Chứng minh HB=HC
c. Chứng minh tam giác HIB= tam giác HKC
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
b) Ta có: ΔABH=ΔACH(cmt)
nên BH=CH(hai cạnh tương ứng)
c) Xét ΔHIB vuông tại I và ΔHKC vuông tại K có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔHIB=ΔHKC(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)




