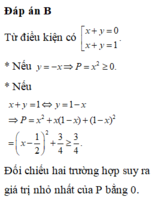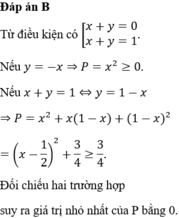Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. CMR giá trị nhỏ nhất của P bằng 0.
UN
Những câu hỏi liên quan
Câu 14. Cho biểu thức P x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:x2 + 4y2 + z2 – 2a + 8y – 6z + 15 0Câu 16. Tìm giá trị lớn nhất của biểu thức:Câu 17. So sánh các số thực sau (không dùng máy tính):Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3Câu 19. Giải phương trình: .Câu 20. Tìm giá trị lớn nhất của biểu thức A x2y với các điều kiện x, y 0 và 2x + x...
Đọc tiếp
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 16. Tìm giá trị lớn nhất của biểu thức:![]()
Câu 17. So sánh các số thực sau (không dùng máy tính):
Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 19. Giải phương trình: ![]() .
.
Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Câu 21. Cho ![]() .
.
Hãy so sánh S và ![]() .
.
Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng:
Câu 24. Chứng minh rằng các số sau là số vô tỉ:
Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?
Câu 26. Cho các số x và y khác 0. Chứng minh rằng:
![]()
Câu 27. Cho các số x, y, z dương. Chứng minh rằng:
![]()
Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 29:
a: \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
\(\Leftrightarrow-a^2+2ab-b^2\le0\)
\(\Leftrightarrow-\left(a-b\right)^2\le0\)(luôn đúng)
Đúng 1
Bình luận (0)
Câu 14. Cho biểu thức P x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:x2 + 4y2 + z2 – 2a + 8y – 6z + 15 0Câu 16. Tìm giá trị lớn nhất của biểu thức:Câu 17. So sánh các số thực sau (không dùng máy tính):Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3Câu 19. Giải phương trình: .Câu 20. Tìm giá trị lớn nhất của biểu thức A x2y với các điều kiện x, y 0 và 2x + x...
Đọc tiếp
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 16. Tìm giá trị lớn nhất của biểu thức:![]()
Câu 17. So sánh các số thực sau (không dùng máy tính):
Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 19. Giải phương trình: ![]() .
.
Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Câu 21. Cho ![]() .
.
Hãy so sánh S và ![]() .
.
Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng:
Câu 24. Chứng minh rằng các số sau là số vô tỉ:
Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?
Câu 26. Cho các số x và y khác 0. Chứng minh rằng:
![]()
Câu 27. Cho các số x, y, z dương. Chứng minh rằng:
![]()
Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
\(14,P=x^2+xy+y^2-3x-3y+3\\ P=\left(x^2+xy+\dfrac{1}{4}y^2\right)-3\left(x+\dfrac{1}{2}y\right)+\dfrac{3}{4}y^2-\dfrac{3}{2}y+3\\ P=\left(x+\dfrac{1}{2}y\right)^2-3\left(x+\dfrac{1}{2}y\right)+\dfrac{9}{4}+\dfrac{3}{4}\left(y^2-2y+1\right)\\ P=\left(x+\dfrac{1}{2}y-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(y-1\right)^2\ge0\)
Đúng 2
Bình luận (0)
14,P=x2+xy+y2−3x−3y+3P=(x2+xy+41y2)−3(x+21y)+43y2−23y+3P=(x+21y)2−3(x+21y)+49+43(y2−2y+1)P=(x+21y−23)2+43(y−1)2≥0
thế này nhé bạn nhé
Đúng 0
Bình luận (0)
cho hai số thực x>0,y>0 thoả mãn xy=6.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
Đúng 1
Bình luận (0)
Câu 1. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 2. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 3. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Hãy giải ba câu hỏi này
Bài 2:
Ta có: M = a2+ab+b2 -3a-3b-3a-3b +2001
=> 2M = ( a2 + 2ab + b2) -4.(a+b) +4 + (a2 -2a+1)+(b2 -2b+1) + 3996
2M= ( a+b-2)2 + (a-1)2 +(b-1)2 + 3996
=> MinM = 1998 tại a=b=1
Câu 3:
Ta có: P= x2 +xy+y2 -3.(x+y) + 3
=> 2P = ( x2 + 2xy +y2) -4.(x+y) + 4 + (x2 -2x+1) +(y2 -2y+1)
2P = ( x+y-2)2 +(x-1)2+(y-1)2
=> MinP = 0 tại x=y=1
Bài1:
Ta có: a2+ b2+c2+d2= a.(b+c+d)
=> a2+b2+c2+d2 -ab -ac -ad =0
=> 4a2+ 4b2+4c2+4d2-4ab -4ac -4ad=0
=> ( a2 - 4ab +4b2) + ( a2- 4ac + 4c2) +( a2 -4ad+ 4d2) + a2=0
=> ( a-2b)2 + ( a-2c)2 + (a-2d)2 + a2 =0
=> ....
KL: a=b=c=d=0
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P = x 2 + x y + y 2 bằng
A. 3 4
B. 0
C. 1 4
D. 1 2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức P
x
2
+
x
y...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P= x 2 + x y + y 2 bằng
A. 3 4
B. 0.
C. 1 4
D. 1 2
Cho x, y ∈ R thỏa mãn x + y + xy = 5 4 . Tìm giá trị nhỏ nhất của biểu thức A = x 2 + y 2
Ta có: 2 x 2 + 1 2 ≥ 2 x ; 2 y 2 + 1 2 ≥ 2 y và x 2 + y 2 ≥ 2 x y
Cộng vế với vế các BĐT trên ta được:
3 x 2 + y 2 + 1 ≥ 2 x + y + x y = 5 2
=> A = x 2 + y 2 ≥ 1 2
Từ đó tìm được A m i n = 1 2 <=> x = y = 1 2
Đúng 0
Bình luận (0)
Giúp e vs plzz sắp thi vào 10 chuyên rồi
Cho x,y là các số thực thay đổi thỏa mãn điều kiện x2 +y2+xy=3.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức x2+y2-xy
\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đúng 2
Bình luận (0)
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đúng 3
Bình luận (0)
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4