TL
Những câu hỏi liên quan
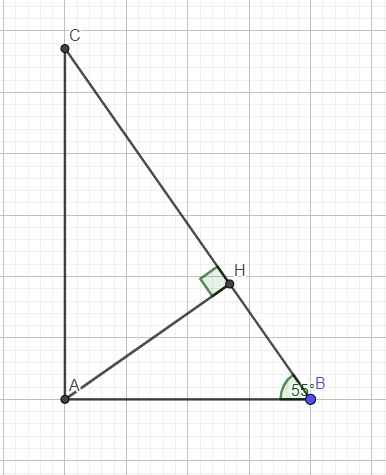
tam giác abc (góc a =90 độ) góc B=55 độ, bc=6 cm. kẻ AH vuông góc với bc. tính AH, BH, HC
Trong tam giác vuông ABC:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB\)
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=BC.sinB.cosB=6.sin55^0.cos55^0\approx2,8\left(cm\right)\)
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=BC.\left(cosB\right)^2=6.\left(cos55^0\right)^2\approx1,2\left(cm\right)\)
\(CH=BC-BH=6-1,2=4,8\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có Â vuông. Từ A kẻ AH vuông góc BC. Biết AB=29cm, AC= 40cm, AH= 1/2 AC. Tính BH và HC
Cho tam ABC có góc A tù.Từ A hạ AH vuông góc BC (H thuộc BC.Biết AB =29cm,AC =40 cm và AH =1/2 BC.Tính BH và HC
Đúng 1
Bình luận (0)
Cho tam giác ABC, góc A=90 độ, AH vuông góc với BC biết AH=30cm , AB/AC =5/6. tính hb hc
Xét \(\Delta ABH\)và \(\Delta CAH\)có
\(\widehat{AHB}=\widehat{CHA}=90^0\)
\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ với góc HAC)
suy ra: \(\Delta ABH~\Delta CAH\) (g.g)
suy ra: \(\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\)
hay \(\frac{5}{6}=\frac{30}{CH}=\frac{BH}{30}\)
suy ra: \(CH=\frac{6.30}{5}=36\)
\(BH=\frac{5.30}{6}=25\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB = AC = 5cm, kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: BH = HC và góc BAH = góc CAH
b) Tính độ dài BH biết AH = 4cm.
c) Kẻ HD vuông góc với AB (D thuộc AB), kẻ EH vuông góc với AC (E thuộc AC). Tam giác ADE là tam giác gì ? Vì sao ?
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC có Â tù. Từ A kẻ AH vuông góc BC. Biết AB=29cm, AC= 40cm, AH= 1/2 BC. Tính BH và HC
KO SAI ĐÂU mik cũng cs đề như thế
cho tam giác abc có ab=30cm kẻ ah vuông góc bc tại h biết bh=18cm hc=32cm
a) tính độ dài ah,ac
b) chứng minh tam giác abc là tam giác vuông
GIÚP MIK LẸ
a) áp dụng đ/l pitago zô tam giác zuông abh ta đc
=> AB^2=AH^2+HB^2
=> AH^2=Ab^2-HB^2
=> AH=24
áp dụng dl pitago zô tam giác zuông ahc
=> AC^2=AH^2+HC^2
=> AC=40
b) Tco : CH+HB=32+18=50
Tam giac ABC có
\(\hept{\begin{cases}AB^2+AC^2=40^2+30^2=2500\\BC^2=50^2=2500\end{cases}}\)
=> \(AB^2+AC^2=BC^2\)
=> tam giác abc zuông
CHo Tam giác ABC, góc A=90, AH vuông góc BC , BH=3,6cm ; HC=6,4cm. Tính BC, AB, AC, AH
Ta có: BC=BH+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8cm\\AB=6cm\\AC=8cm\end{matrix}\right.\)
Đúng 1
Bình luận (0)
BC=BH+HC=3,6+6,4=10CM
AB^2=BH.BC
=>AB=6CM
AC=\(\sqrt{BC^2-AB^2}=8CM\)
AH^2=BH.HC
=>AH=4,8CM
Đúng 1
Bình luận (0)
đề 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC,AB=30cm,AH=24cm.
a)tính BH?BC?
b)tính các tỉ số lượng giác của các góc của tam giác AHB
đề 2
cho tam giác ABC vuông tại A, AH vuông góc BC , HB=4cm, HC=9cm
a)tính các cạnh tam giác ABC
b)tính các góc của tam giác ABC
cho tam giác cân ABC có ABC : AB=AC=10cm , BC=12cm , gọi AH là tia phân giác góc A (H thuộc BC)
a. CM BH=HC và AH vuông góc BC
b. Tính độ dài AH
c. Kẻ HD vuông góc AB (D thuộc AB) HE vuông góc AC (E thuộc AC).Hỏi tam giác DHE là tam giác gì ?
d. CM DE//BC
Giúp mình với ạ 😭✨
a: ΔABC cân tại A có AH là phân giác
nên H là trung điểm của BC
ΔABC cân tại A có AH là trung tuyến
nên AH vuông góc BC
b: BH=CH=12/2=6cm
AH=căn AB^2-AH^2=8cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>AD=AE và HD=HE
=>ΔHDE cân tại H
d: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Đúng 0
Bình luận (0)