tìm tát cả các nghiệm x thuộc (2009,2011) của phương trình : |cos|-|sinx|-cos2x*căn(1+sin2x) = 0
H24
Những câu hỏi liên quan
1. Cos² 3x = 1
2.Sinx = 1 - cos²x
3.Tìm nghiệm € (0;2x) của phương trình cos - 2x + sinx=0
4.Sin2x + sinx = 0
5.căn 2 cos (x+pi/3) = 1
1: =>sin^2(3x)=0
=>sin 3x=0
=>3x=kpi
=>x=kpi/3
2:
\(sinx=1-cos^2x=sin^2x\)
=>\(sin^2x-sinx=0\)
=>sin x(sin x-1)=0
=>sin x=0 hoặc sin x=1
=>x=pi/2+k2pi hoặc x=kpi
4:
sin 2x+sin x=0
=>sin 2x=-sin x=sin(-x)
=>2x=-x+k2pi hoặc 2x=pi+x+k2pi
=>x=pi+k2pi hoặc x=k2pi/3
5: =>cos(x+pi/3)=1/căn 2
=>x+pi/3=pi/4+k2pi hoặc x+pi/3=-pi/4+k2pi
=>x=-pi/12+k2pi hoặc x=-7/12pi+k2pi
Đúng 0
Bình luận (0)
1, cho phương trình sin2x-left(2m+sqrt{2}right)left(sinx+cosxright)+2msqrt{2}+10 tìm các giá trị m để phương trình có đúng 2 nghiệm xinleft(0;dfrac{5Pi}{4}right)2,tìm tất cả các giá trị thực của tham số m để phương trình cos2x+left(2m+1right)sinx-m-10 có đúng 2 nghiệm thuộc khoảng left(dfrac{Pi}{2};dfrac{3Pi}{2}right)3, cho phương trình cos^2x-2mcosx+6m-90 tìm các giá trị m để phương trình có nghiệm thuộc khoảng left(-dfrac{Pi}{2};dfrac{Pi}{2}right)
Đọc tiếp
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Tìm nghiệm x của phương trình
2
sin
3
x
+
sin
2
x
-
sin
x
+
1
3
-
2
sin
x
-
cos
2
x
Đọc tiếp
Tìm nghiệm x của phương trình
2 sin 3 x + sin 2 x - sin x + 1 = 3 - 2 sin x - cos 2 x
![]()
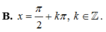
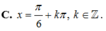

Gọi S là tâp hợp tất cả các nghiệm thuộc khoảng (0;2018) của phương trình lượng giác
3
(
1
-
cos
2
x
)
+
sin
2
x
-
4
cosx
+
8
4
(
3
+
1
)
sinx
. Tính tổng tất cả các phần tử của S là A.
310408
3
π
B. ...
Đọc tiếp
Gọi S là tâp hợp tất cả các nghiệm thuộc khoảng (0;2018) của phương trình lượng giác 3 ( 1 - cos 2 x ) + sin 2 x - 4 cosx + 8 = 4 ( 3 + 1 ) sinx . Tính tổng tất cả các phần tử của S là
A. 310408 3 π
B. 102827 π
C. 312341 3 π
D. 104760 π
Tìm nghiệm x của phương trình
2
sin
3
x
+
sin
2
x
-
s
i
n
x
+
1
3-2sinx-
cos
2
x
thỏa mãn điều kiện
s...
Đọc tiếp
Tìm nghiệm x của phương trình 2 sin 3 x + sin 2 x - s i n x + 1 = 3-2sinx- cos 2 x
thỏa mãn điều kiện sin x < 1 2
![]()
![]()
![]()
![]()
Đáp án A
Phương trình đã cho tương đương với
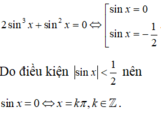
Đúng 0
Bình luận (0)
Tìm nghiệm x của phương trình
2
(
sin
3
x
+
sin
2
x
-
sin
x
+
1
)
3
-
2
sin
x
-
cos
2
x
thỏa mãn điều kiện
sin
x...
Đọc tiếp
Tìm nghiệm x của phương trình
2 ( sin 3 x + sin 2 x - sin x + 1 ) = 3 - 2 sin x - cos 2 x
thỏa mãn điều kiện sin x < 1 2
A. x = kπ ; k ∈ ℤ
B. x = π 2 + k π ; k ∈ ℤ
C. x = π 6 + k π ; k ∈ ℤ
D. x ∈ ∅
Phương trình đã cho tương đương với
2 sin 3 x + sin 2 x = 0 ⇔ sin x = 0 sin x = - 1 2
Do điều kiện
sin
x
<
1
2
nên sinx = 0 nên
x
=
kπ
;
k
∈
ℤ
Đáp án A
Đúng 0
Bình luận (0)
a)căn 3 sin4x-cos4x-2cosx=0
b)cosx +căn 3 cos2x-căn 3 sinx-sin2x=0
c)cos 3x+sin2x=căn 3(sin3x+cos2x)
d)cosx +căn 3=3-3/cosx+căn 3 sinx+1
a/
\(\sqrt{3}sin4x-cos4x=2cosx\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin4x-\frac{1}{2}cos4x=cosx\)
\(\Leftrightarrow sin\left(4x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\frac{\pi}{6}=\frac{\pi}{2}-x+k2\pi\\4x-\frac{\pi}{6}=\frac{\pi}{2}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2\pi}{15}+\frac{k2\pi}{5}\\x=\frac{2\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/
\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x-\sqrt{3}cos2x\)
\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=sin\left(2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(\frac{\pi}{6}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}-x+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow cos3x-\sqrt{3}sin3x=\sqrt{3}cos2x-sin2x\)
\(\Leftrightarrow\frac{1}{2}cos3x-\frac{\sqrt{3}}{2}sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(3x+\frac{\pi}{3}\right)=cos\left(2x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\3x+\frac{\pi}{3}=-2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=-\frac{\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tất cả giá trị của m để phương trình sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m có nghiệm?
A. 0 ≤ m ≤ 1
B.m> 1
C.0< m< 1
D. m ≤ 0
Hướng dẫn giải:
Chọn A.
Ta có: sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m
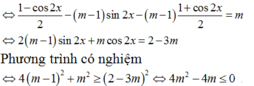
![]()
Đúng 0
Bình luận (0)
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(x-dfrac{pi}{4}) sqrt{2}sinx trên đoạn [0 ; 2018]Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) cos3x - cos2x + 1 trên đoạn [0 ; 43π]GIÚP MÌNH VỚI!!!
Đọc tiếp
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(\(x-\dfrac{\pi}{4}\)) = \(\sqrt{2}\)sinx trên đoạn [0 ; 2018]
Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) = cos3x - cos2x + 1 trên đoạn [0 ; 43π]
GIÚP MÌNH VỚI!!!![]()




