cho tam giác ABC có các cạnh thỏa
a(a2-b2)=c(b2-c2).Tính góc B
Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
Chọn B.
Ta có:
a(a2 – c2) = b(b2 – c2) ⇔ a3 – ac2 = b3 – bc2
⇔ a3 – b3 = ac2 – bc2
⇔ (a – b)(a2 + ab + b2) = c2(a – b)
⇔ a2 + ab + b2 = c2
⇔ ab = c2 – a2 – b2
Ta lại có: 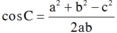
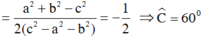
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
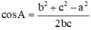
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Cho tam giác ABC. Biết các cạnh a, b, c thoả mãn hệ thức: b(b2 - a2) = c(c2 - a2). Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân
C. Tam giác ABC là tam giác tù
D. tam giác ABC là tam giác nhọn
Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.
Cho tam giác ABC có AB=a, AC=b, AB=c. Biết b(b2- a2)=c(a2 -c2). Số đo của góc A bằng
A. 30 °
B. 60 °
C. 150 °
D. 120 °
Cho tam giác ABC có a2 = b2 + c2 − bc. Góc B bằng bao nhiêu?
A. 1500 B. 1200 C. 600 D. 300
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
cho a,b,c là độ dài 3 cạnh tam giác.
a)a2/b2+b2/a2≥ a/b+b/a
b)a2/b+b2/a+c2/a≥ a+b+c
c)a2/(b+c)+b2/(a+c)+c2/(a+b)≥ (a+b+c)/2
cho tam giác ABC, góc A=120 độ, AB=c, BC=a, AC=b. C/m: a2=b2+c2+bc
tam giác ABC có 3 cạnh a,b,c
a) a2+b2+c2< 2(ab+bc+ca)
b) abc\(\ge\)(a+b-c)(b+c-a)(c+a-b)
a.
Theo BĐT tam giác: \(c< a+b\Rightarrow c^2< ac+bc\)
\(b< a+c\Rightarrow b^2< ab+bc\) ; \(a< b+c\Rightarrow a^2< ab+ac\)
Cộng vế với vế: \(a^2+b^2+c^2< 2\left(ab+bc+ca\right)\)
b.
Do a;b;c là 3 cạnh của tam giác nên: \(\left\{{}\begin{matrix}a+b-c>0\\b+c-a>0\\c+a-b>0\end{matrix}\right.\)
\(\left(a+b-c\right)\left(b+c-a\right)\le\dfrac{1}{4}\left(a+b-c+b+c-a\right)^2=b^2\)
Tương tự: \(\left(b+c-a\right)\left(a+c-b\right)\le c^2\) ; \(\left(a+b-c\right)\left(a+c-b\right)\le a^2\)
Nhân vế với vế:
\(\left(abc\right)^2\ge\left[\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\right]^2\)
\(\Leftrightarrow abc\ge\left(a+b-c\right)\left(c+a-b\right)\left(b+c-a\right)\)