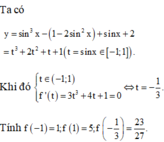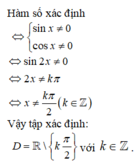PP
Những câu hỏi liên quan
Giá trị lớn nhất của hàm số y = sin 3 x -cos2x+sinx+2 trên tập xác định của nó là
A. -1
B. 5
C. 3
D. 1
Giá trị lớn nhất của hàm số y = sin 3 x − cos 2 x + sin x + 2 trên tập xác định của nó là
A. -1
B. 5
C. 3
D. 1
Đáp án B.
Ta có
y = sin 3 x − 1 − 2 sin 2 x + s inx + 2 = t 3 + 2 t 2 + t + 1 t = s inx ∈ − 1 ; 1 .
Khi đó t ∈ − 1 ; 1 f ' t = 3 t 3 + 4 t + 1 = 0 ⇔ t = − 1 3 .
Tính f − 1 = 1 ; f 1 = 5 ; f − 1 3 = 23 27 .
Đúng 0
Bình luận (0)
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Tìm tập xác định và tập giá trị của mỗi hàm số sau:
a) \(y=2x+3\);
b) \(y=2x^2\).
a) Biểu thức \(2x + 3\) có nghĩa với mọi x, nên có tập xác định \(D = \mathbb{R}\)
Do đó tập giá trị của hàm số là \(\mathbb{R}\)
b) Biểu thức \(2{x^2}\) có nghĩa với mọi x, nên có tập xác định \(D = \mathbb{R}\)
Ta có: \({x^2} \ge 0\) Do đó \(y = 2{x^2} \ge 0\), tập giá trị của hàm số là \(\left[ {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số y=2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là R.
B. Tập giá trị của hàm số là (0;+∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
Đúng 0
Bình luận (0)
Cho hàm số y=\(\left\{{}\begin{matrix}\dfrac{2x-3}{x-1}khix\ge2\\x^3-3xkhĩ< 2\end{matrix}\right.\) Khẳng định nào sau đây là khẳng định sai?
A.Tập hợp xác định của hàm số là R
B. Tập xác định của hàm số là R\\(\left\{1\right\}\)
C. Giá trị của hàm số tại x=2 bằng 1
D. Giá trị của hàm số tại x=1 bằng -2
`C.x=2=>y=(2.2-3)/(2-1)=1=>Đ`
`D.x=1=>y=1^3-3=-2=>Đ`
`A.TXĐ:RR=>Đ`
`=>B.` sai
Đúng 1
Bình luận (0)
Tập xác định của hàm số y = 2 tanx – 3cot x là
A. R
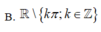
![]()
Tìm tập xác định của hàm số
1/ \(y=\dfrac{sinx}{\sqrt{3-cosx}}\)
2/ \(y=\sqrt{1-sin3x}\)
3/ \(y=\dfrac{tan2x+1}{sinx}\)
4/ \(y=sin\sqrt{2x-1}\)
1: ĐKXĐ: 3-cosx>0
=>cosx<3(luôn đúng)
2: ĐKXĐ: 1-sin 3x>=0
=>sin 3x<=1(luôn đúng)
3: ĐKXĐ: sin x<>0 và 2x<>pi/2+kpi
=>x<>kpi và x<>pi/4+kpi/2
4: ĐKXĐ: 2x-1>=0
=>x>=1/2
Đúng 1
Bình luận (0)