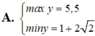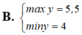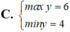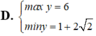với x>3 tìm min của
M=x2+2x-9/x-3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
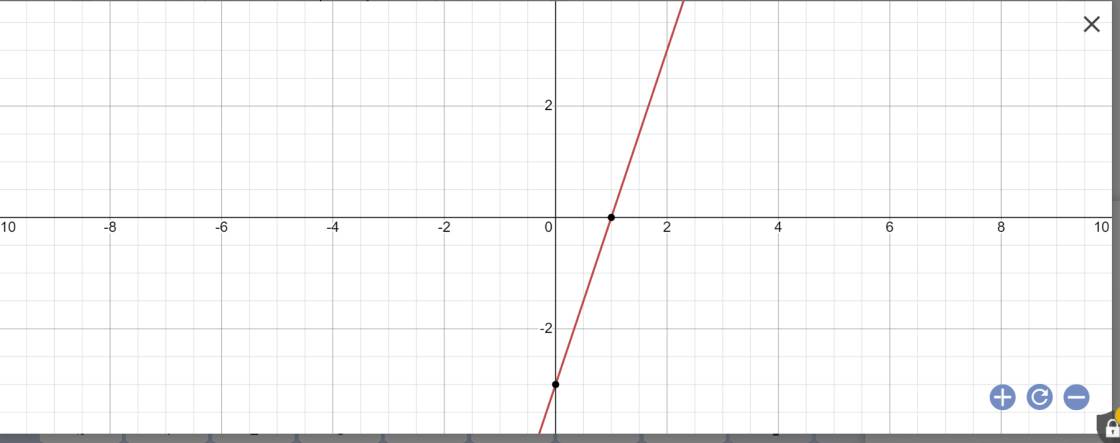
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Tìm đa thức M biết:
a) 2 x 3 + 9 x 2 + 15x + 9 = M.(2x + 3);
b) (2 x 2 - 2x +1 ).M = 6 x 4 - 4 x 3 + x 2 + x.
Tìm min của biểu thức(áp dụngBđtCauchy)
Q= (x2 + 2x+1)/(x+2)
R= (x2 -x+4)+ 1/( x 2 -x -1)
S=(x2 +x+1)/ (x2 +2x+1)
TÌM MAX CỦA BIỂU THỨc
A= x/(x+2004)2 với x>0
B= 3/(4x2 - 4x+5)
C= (x2 -6x+14)/ (x2- 6x+12)
Giúp mk với, đúng mình tick cho , mình cần gấp lắm, làm câu nào cũng được nhé!! Được hết ccàng tốt)
1) tìm giá trị nhỏ nhất của
D= 4x-x2+3
E=2x-2x2-5
F=-x2-4x+20
2) chứng minh biểu thức không phụ vào biến
A= (2x+3)(4x2-6x+9)-2(4x3-1)
B=(x+3)3-(x+9)(x2+27)
1. Đề bài sai, các biểu thức này chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất
2.
\(A=\left(2x\right)^3-3^3-\left(8x^3+2\right)\)
\(=8x^3-27-8x^3-2\)
\(=-29\)
\(B=x^3+9x^2+27x+27-\left(x^3+9x^2+27x+243\right)\)
\(=27-243=-216\)
sửa đề lại thành tìm Max nhé1, vì mấy ý này ko có min
\(1,=>D=-\left(x^2-4x-3\right)=-\left(x^2-2.2x+4-7\right)\)
\(=-[\left(x-2\right)^2-7]=-\left(x-2\right)^2+7\le7\)
dấu"=" xảy ra<=>x=2
2, \(E=-2\left(x^2-x+\dfrac{5}{2}\right)=-2[x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4}]\)
\(=-2[\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}]\le-\dfrac{9}{2}\) dấu"=" xảy ra<=>x=1/2
3, \(F=-\left(x^2+4x-20\right)=-\left(x^2+2.2x+4-24\right)\)
\(=-[\left(x+2\right)^2-24]\le24\) dấu"=" xảy ra<=>x=-2
Bài 1:
a) Ta có: \(D=-x^2+4x+3\)
\(=-\left(x^2-4x-3\right)\)
\(=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\forall x\)
Dấu '=' xảy ra khi x=2
c) Ta có: \(F=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2
Bài 5. Tìm x , biết rằng: a) x(x + 5)(x – 5) – (x + 2)(x2 – 2x + 4) = 3
b) (x – 3)3 – (x – 3)(x2 + 3x + 9) + 9(x + 1)2 = 15
c) (x+5)(x2 –5x +25) – (x – 7) = x3
d) (x+2)(x2 – 2x + 4) – x(x2 + 2) = 4
`a) x(x + 5)(x – 5) – (x + 2)(x^2 – 2x + 4) = 3`
`<=>x(x^2-25)-(x^3-8)=3`
`<=>x^3-25x-x^3+8=3`
`<=>-25x=-5`
`<=>x=1/5`
`b) (x – 3)^3 – (x – 3)(x^2 + 3x + 9) + 9(x + 1)^2 = 15`
`<=>x^3-9x^2+27x-27-(x^3-27)+9(x^2+2x+1)=15`
`<=>-9x^2+27x+9x^2+18x+9=15`
`<=>45x+9=15`
`<=>45x=6`
`<=>x=6/45=2/15`
`c) (x+5)(x^2 –5x +25) – (x – 7) = x^3`
`<=>x^3-125-x+7=x^3`
`<=>x^3-x-118=x^3`
`<=>-x-118=0`
`<=>-x=118<=>x=-118`
`d) (x+2)(x^2 – 2x + 4) – x(x^2 + 2) = 4 `
`<=>x^3+8-x^3-2x=4`
`<=>8-2x=4`
`<=>2x=4<=>x=2`
Tìm x biết:
a) ( x – 3 ) 3 – ( x – 3 ) ( x 2 + 3 x + 9 ) + 9 ( x + 1 ) 2 = 15;
b) x(x – 5)(x + 5) – (x + 2)( x 2 - 2x + 4) = 3.
a) Rút gọn VT = 45x + 8. Từ đó tìm được x = 2 15 .
b) Rút gọn VT = -25x – 8. Từ đó tìm được x = − 11 25 .
Tìm x :
a) x (3x + 1) + (x -1)2 - (2x + 1)(2x -1) = 0
b) (x + 1)3 + (2 - x)3 - 9(x - 3)(x+3) = 0
c) (x - 1)3 - (x + 3)(x2 - 3x + 9) + 3x2 = 25
d) (x + 2)3 - ( x +1)(x2 - x + 1) - 6(x - 1)2 = 23
e) (x + 3)(x2 - 3x + 9) - x(x - 2)(x+2) + 11 = 0
f) x(x - 3) - x + 3 = 0
Lời giải:
a. $x(3x+1)+(x-1)^2-(2x+1)(2x-1)=0$
$\Leftrightarrow (3x^2+x)+(x^2-2x+1)-(4x^2-1)=0$
$\Leftrightarrow 3x^2+x+x^2-2x+1-4x^2+1=0$
$\Leftrightarrow (3x^2+x^2-4x^2)+(x-2x)+(1+1)=0$
$\Leftrightarrow -x+2=0$
$\Leftrightarrow x=2$
b.
$(x+1)^3+(2-x)^3-9(x-3)(x+3)=0$
$\Leftrightarrow [(x+1)+(2-x)][(x+1)^2-(x+1)(2-x)+(2-x)^2]-9(x-3)(x+3)=0$
$\Leftrightarrow 3[x^2+2x+1-(x-x^2+2)+(x^2-4x+4)]-9(x-3)(x+3)=0$
$\Leftrightarrow 3(3x^2-3x+3)-9(x^2-9)=0$
$\Leftrightarrow 9(x^2-x+1)-9(x^2-9)=0$
$\Leftrightarrow 9(x^2-x+1-x^2+9)=0$
$\Leftrightarrow 9(-x+10)=0$
$\Leftrightarrow -x+10=0\Leftrightarrow x=10$
c.
$(x-1)^3-(x+3)(x^2-3x+9)+3x^2=25$
$\Leftrightarrow (x^3-3x^2+3x-1)-(x^3+3^3)+3x^2=25$
$\Leftrightarrow x^3-3x^2+3x-1-x^3-27+3x^2=25$
$\Leftrightarrow (x^3-x^3)+(-3x^2+3x^2)+3x-28=25$
$\Leftrightarrow 3x-28=25$
$\Leftrightarrow x=\frac{53}{3}$
d.
$(x+2)^3-(x+1)(x^2-x+1)-6(x-1)^2=23$
$\Leftrightarrow (x^3+6x^2+12x+8)-(x^3+1)-6(x^2-2x+1)=23$
$\Leftrightarrow x^3+6x^2+12x+8-x^3-1-6x^2+12x-6=23$
$\Leftrightarrow (x^3-x^3)+(6x^2-6x^2)+(12x+12x)+(8-1-6)=23$
$\Leftrightarrow 24x+1=23$
$\Leftrgihtarrow 24x=22$
$\Leftrightarrow x=\frac{11}{12}$
e.
$(x+3)(x^2-3x+9)-x(x-2)(x+2)+11=0$
$\Leftrightarrow x^3+3^3-x(x^2-4)+11=0$
$\Leftrightarrow x^3+27-x^3+4x+11=0$
$\Leftrightarrow (x^3-x^3)+4x+(27+11)=0$
$\Leftrightarrow 4x+38=0$
$\Leftrightarrow x=\frac{-19}{2}$
f.
$x(x-3)-x+3=0$
$\Leftrightarrow x(x-3)-(x-3)=0$
$\Leftrightarrow (x-3)(x-1)=0$
$\Leftrightarrow x-3=0$ hoặc $x-1=0$
$\Leftrightarrow x=3$ hoặc $x=1$
Bài 1: Tìm x:
1) (x-3)3 -( x-3)(x2+ 3x+9) +6( x+1)2+ 3x2 = -33
2) (X-3)( X2+ 3X+9) - X(X-2)( 2+X) = 1
3) (X+2)(X2 - 2X+4) – X(X-3)(X+3) = 26
a: Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2+3x^2=-33\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+6x^2+12x+1+3x^2=-33\)
\(\Leftrightarrow39x=-34\)
hay \(x=-\dfrac{34}{39}\)
b: Ta có: \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x-2\right)\left(x+2\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
\(\Leftrightarrow4x=28\)
hay x=7
c: Ta có: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-3\right)\left(x+3\right)=26\)
\(\Leftrightarrow x^3+8-x^3+9x=26\)
\(\Leftrightarrow x=2\)
Tìm GTLN (max), GTNN (min) của y = x 2 - x + 2 x - 1 khi x ∈ 3 2 ; 3