Cho tứ giác ABCD có ;
;
. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
a. Tính số đo góc C
b. Chứng minh tứ giác EFGH là hình bình hành.
c. Biết đường chéo AC = 18cm.Tính độ dài đoạn thẳng EF.
Câu 32. Cho tứ giác ABCD có AB//CD và góc A= góc B , hãy chọn khẳng định đúng
A. Tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình thang cân.
C. Tứ giác ABCD là hình thang vuông.
D. Tứ giác ABCD có góc bằng nhau.
B. Tứ giác ABCD là hình thang cân.
Cho tứ giác ABCD có AC = BD và AC vuông góc BD. khi đó : A. Tứ giác ABCD là hình vuông B. Tứ giác ABCD là hình bình hành C. Tứ giác ABCD là hình thoi D. ABCD là tứ giác bất kì
Cho tứ giác lồi ABCD, lấy E và F là trung điểm của AB và CD. Biết EF chia tứ giác ABCD thành hai tứ giác có diện tích bằng nhau. Chứng minh tứ giác ABCD là hình thang.
ta có diện tích hai tam giác AFE bằng BFE ( do tam giác ABF có đường trung tuyến FE)
kết hợp với giả thiết ta có diện tích ADF bằng BCF
hay d(A,DF).DF.1/2=d(B,CF).CF.1/2
hay d(A,DF)=d(B,CF)d(A,DF)=d(B,CF) hay AB song song với DC
vậy => đpcm
Cho tứ giác ABCD có : góc A : B : C : D = 2 : 3 : 4 : 5.Tính số đo các góc của tứ giác .Khi đó tứ giác ABCD có gì đặc biệt
Ta co A:B:C;D = 2:3:4:5
\(\Rightarrow\)\(\dfrac{A}{2}\) = \(\dfrac{B}{3}\) = \(\dfrac{C}{4}\) = \(\dfrac{D}{5}\) = \(\dfrac{A+B+C+D}{2+3+4+5}\) = \(\dfrac{360}{14}\) = \(\dfrac{180}{7}\)
\(\Rightarrow\) A= \(\dfrac{180}{7}\). 2 \(\approx\) 51
B= \(\dfrac{180}{7}\). 3 \(\approx\) 77
C= \(\dfrac{180}{7}\). 4 \(\approx\) 103
D= \(\dfrac{180}{7}\). 5 \(\approx\) 129
Ta thay: A+D=180 ; B+C=180 \(\Rightarrow\) ABCD la hinh thang
Cho tứ giác ABCD có ^A=^B=^C=^D.Tính số đo của các góc tứ giác ABCD
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\)
Cho tứ giác ABCD. Dựng hình bình hành ABCD. Chứng minh rằng tứ giác ABCD và tam giác ACC' có diện tích bằng nhau ?
Cho tứ giác ABCD có BD là phân giác ∠B và BC = CD. Chứng minh tứ giác ABCD là hình thang.
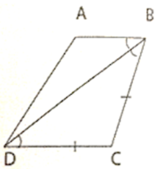
Vì BD là phân giác của ∠ABC
Suy ra ∠ABD = ∠CBD (1)
Lại có BC = CD (gt)
Suy ra ΔCBD cân tại C
Nên ∠CBD = ∠CDB (2)
Từ (1) và (2) suy ra:
∠ABD = ∠CDB Mà 2 góc này ở vị trí so le trong
Suy ra AB // CD
Vậy ABCD là hình thang.
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình chữ nhật?
c) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình thoi?
Nối B với D
Xét ΔABD có :
AM = BM (gt)
AQ = DQ (gt)
=> QM là đường tb của ΔABD
=> QM // BD , QM = 1/2 BD(1)
Chứng minh tương tự ΔBCD
=> NP là đường tb của ΔBCD
=> NP // BD , NP = 1/2 BD (2)
Từ (1) và (2 ) => Tứ giác MNPQ là hình bình hành (dhnb)(đcpcm)
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình chữ nhật?
c) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình thoi?
giúp mik vẽ hình và lời giải chiều ni mik nộp rồi
Cho tứ giác ABCD có AM = MN = ND; PB = PQ = QC. Hãy chứng tỏ diện tích tứ giác MNQP = 1/3 diện tích tứ giác ABCD