Tìm \(GTLN\) của biểu thức: \(-\left|3+x\right|+2\)
RM
Những câu hỏi liên quan
a) Tìm GTNN của biểu thức \(C=\left(x+1\right)^2+\left(y-\frac{1}{3}\right)^2-10\)
b)Tìm GTLN của biểu thức \(D=\frac{5}{\left(2x-1\right)^2+3}\)
Câu hỏi của đào mai thu - Toán lớp 7 - Học toán với OnlineMath
eM THAM khảo nhé!
Đúng 0
Bình luận (0)
1. Cho số nguyên dương x.a, Tìm GTNN của biểu thức Psqrt[3]{10^x-2}+sqrt{x^x+3}+sqrt{left(pi^2+1right)^{x-1}+3}.b, Tìm GTLN của biểu thức Qsqrt[5]{left(6x^2+5right)^{1-x}}+sqrt[3]{3-2x^2}.c, Chứng minh rằng: dfrac{left(x+1right)^6}{left(x^3+7right)left(x^3+3x^2+4right)}ge1.2. Cho tam giác OEF vuông tại O có OE a, OF b, EF c thỏa mãn điều kiện a, b, c là các số dương. Chứng minh rằng biểu thức Adfrac{a+b}{c}+dfrac{c}{a+b} không nhận bất kì giá trị nguyên dương nào.
Đọc tiếp
1. Cho số nguyên dương x.
a, Tìm GTNN của biểu thức \(P=\sqrt[3]{10^x-2}+\sqrt{x^x+3}+\sqrt{\left(\pi^2+1\right)^{x-1}+3}\).
b, Tìm GTLN của biểu thức \(Q=\sqrt[5]{\left(6x^2+5\right)^{1-x}}+\sqrt[3]{3-2x^2}\).
c, Chứng minh rằng: \(\dfrac{\left(x+1\right)^6}{\left(x^3+7\right)\left(x^3+3x^2+4\right)}\ge1\).
2. Cho tam giác OEF vuông tại O có OE = a, OF = b, EF = c thỏa mãn điều kiện a, b, c là các số dương. Chứng minh rằng biểu thức \(A=\dfrac{a+b}{c}+\dfrac{c}{a+b}\) không nhận bất kì giá trị nguyên dương nào.
a, Tìm GTLN của biểu thức \(A=\sqrt{3}-\left(x-2\right)^2\)
b, Tìm GTNN của biểu thức \(B=\left(2x-5\right)^2+2019\)
a)\(MaxA=\sqrt{3}\)<=>Dấu ''='' xảy ra
<=>x=2
b) Min A =2019<=>Dấu ''='' xảy ra
<=>2x-5=0
<=>x=5/2
Đúng 0
Bình luận (0)
Tìm GTLN của biểu thức \(M=|x-2|.\left(3-|x-2|\right)\)
đặt Ix-2I=y
ta có M=y(3-y)=3y-y2=-(y2-3y+9/4)+9/4=-(y-3/2)2+9/4
tự giải tiếp
Đúng 0
Bình luận (0)
a. tìm GTNN của biểu thức \(C=\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2-10\)
b. tìm GTLN của biểu thức \(D=\frac{4}{\left(2x-3\right)^2+5}\)
a) Ta có: \(\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2\ge0\)(với mọi x,y)
=>\(C=\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2-10\ge-10\)
Dấu "=" xảy ra khi x=-2;y=1/5
Vậy GTNN của C là -10 tại x=-2;y=1/5
Đúng 0
Bình luận (0)
b)Ta có: \(\left(2x-3\right)^2\ge0\Rightarrow\left(2x-3\right)^2+5\ge0\Rightarrow D=\frac{4}{\left(2x-3\right)^2+5}\le\frac{4}{5}\)
Dấu "=" xảy ra khi: x=3/2
Vậy GTLN của D là : 4/5 tại x=3/2
Đúng 1
Bình luận (0)
b)B có GTLN <=> (2x-3)2+5 có GTNN
Vì (2x-3)2 > 0 với mọi x
=>(2x-3)2+5 > 5 với mọi x
=>GTNN của (2x-3)2+5 là 5
=>D = \(\frac{4}{\left(2x-3\right)^2+5}\) < \(\frac{4}{5}\)
=>GTLN của D là 4/5
Dấu "=" xảy ra <=> (2x-3)2=0<=>x=3/2
Vậy..............
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
173. a) Tìm GTNN của biểu thức \(C=\left(x+2\right)^2+\left(y-\frac{1}{5}\right)^2-10\)
b) Tìm GTLN của biểu thức \(D=\frac{4}{\left(2x-3\right)^2+5}\)
Cho biểu thức: K=(\(\dfrac{x^2}{x^2-5x+6}\)+\(\dfrac{x^2}{x^2-3x+2}\)).\(\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+x^2+1}\)
a, Tìm đkxđ rồi rút gọn K
b, Tìm GTLN của K
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
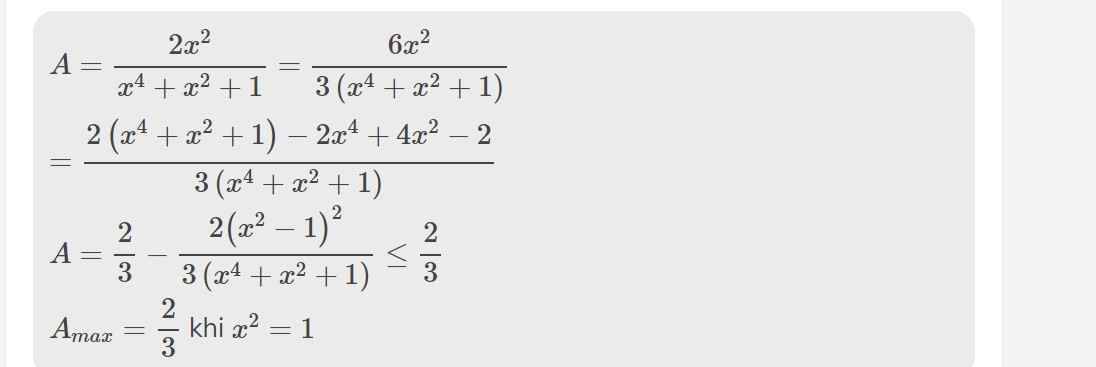
Đúng 0
Bình luận (0)
Tìm GTLN của biểu thức D=\(\left|x-2022\right|\)+\(\left|x-1\right|\)
hellp!!!
Tìm GTNN chứ nhỉ e
\(D=\left|2022-x\right|+\left|x-1\right|\ge\left|2022-x+x-1\right|=2021\)
Dấu "=" xảy ra \(\Leftrightarrow\left(2022-x\right)\left(x-1\right)\ge0\)
\(\Leftrightarrow1\le x\le2022\)
Vậy Min D=2021 \(\Leftrightarrow1\le x\le2022\)
Đúng 2
Bình luận (0)
Giúp mình với :a)Tìm GTNN của A left|x^2-x+1right|+left|x^2-x-2right|b ) tìm GTNLN của D frac{x+2}{left|xright|}với x khác 0 và x thuộc Zc) tìm GTLN của Ffrac{7x-8}{2x-3}với x thuộc Nd) Timf GTNN của Gxleft(x+1right)+x+2e) Tìm GTLN của J x^4+2x^2-7f) Tìm GTLN của biểu thức N left(x+2right)^2-4x+2G ) tìm GTLN của T 4left(3-left|x-1right|right)+left|1-xright|
Đọc tiếp
Giúp mình với :
a)Tìm GTNN của A = \(\left|x^2-x+1\right|+\left|x^2-x-2\right|\)
b ) tìm GTNLN của D =\(\frac{x+2}{\left|x\right|}\)với x khác 0 và x thuộc Z
c) tìm GTLN của F=\(\frac{7x-8}{2x-3}\)với x thuộc N
d) Timf GTNN của G=\(x\left(x+1\right)+x+2\)
e) Tìm GTLN của J = \(x^4+2x^2-7\)
f) Tìm GTLN của biểu thức N = \(\left(x+2\right)^2-4x+2\)
G ) tìm GTLN của T= \(4\left(3-\left|x-1\right|\right)+\left|1-x\right|\)
Tìm GTLN, GTNN của biểu thức sau
\(1,A=\left(x-1\right)^2-10\)
\(2,B=-|x-1|-2\left(2y-1\right)^2+100\)
1: \(A=\left(x-1\right)^2-10\ge-10\)
Dấu '=' xảy ra khi x=1
2: \(B=-\left|x-1\right|-2\cdot\left(2y-1\right)^2+100\le100\)
Dấu '=' xảy ra khi x=1 và y=1/2
Đúng 3
Bình luận (0)
`(x-1)^2 >=0 => (x-1)^2 - 10 >= -10`
Dấu bằng xảy ra khi `x = 1`.
Vì `-|x-1| <=0, -2(2y-1)^2 <= 0`
`=> -|x-1| - 2(2y-1)^2 + 100 <= 100`
Dấu bằng xảy ra `<=> x = 1, y = 1/2`.
Đúng 1
Bình luận (0)




