Giải phương trình f'(x) = 0, biết rằng: f x = 1 - sin π + x + 2 cos 2 π + x 2
PB
Những câu hỏi liên quan
Giải phương trình \(f'\left(x\right)=0\) biết rằng :
a) \(f\left(x\right)=3\cos x+4\sin x+5x\)
b) \(f\left(x\right)=1-\sin\left(\pi+x\right)+2\cos\left(\dfrac{2\pi+x}{2}\right)\)
a) f'(x) = - 3sinx + 4cosx + 5. Do đó
f'(x) = 0 <=> - 3sinx + 4cosx + 5 = 0 <=> 3sinx - 4cosx = 5
<=> sinx -
cosx = 1. (1)
Đặt cos φ = , (φ ∈
) => sin φ =
, ta có:
(1) <=> sinx.cos φ - cosx.sin φ = 1 <=> sin(x - φ) = 1
<=> x - φ = + k2π <=> x = φ +
+ k2π, k ∈ Z.
b) f'(x) = - cos(π + x) - sin = cosx + sin
.
f'(x) = 0 <=> cosx + sin = 0 <=> sin
= - cosx <=> sin
= sin
<=> =
+ k2π hoặc
= π - x +
+ k2π
<=> x = π - k4π hoặc x = π + k, (k ∈ Z).
Đúng 0
Bình luận (0)
Giải phương trình f'(x) = 0, biết rằng f ( x ) = 3 x + 60 x - 64 x 3 + 5
Giải phương trình f(x) 0, biết rằng
f
(
x
)
sin
3
x
3
+
cos
x
-
3
sin
x
+
cos
3...
Đọc tiếp
Giải phương trình f'(x) = 0, biết rằng f ( x ) = sin 3 x 3 + cos x - 3 sin x + cos 3 x 3
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) m có nghiệm thuộc khoảng
0
;
π
là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình bên. Phương trình f( 2 sin x) m có đúng ba nghiệm phân biệt thuộc đoạn
-
π
;
π
khi và chỉ khi A.
m
∈
-
3
;
1
B.
m
∈
-...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
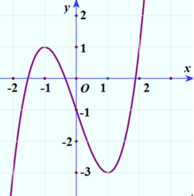
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Cho hàm số: \(f(x)=\dfrac{1}{3}x^3−\dfrac{1}{2}x^2−4x+6\)
a) Giải phương trình \(f’(\sin x) = 0\)
b) Giải phương trình \(f’’(\cos x) = 0\)
c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình \(f’’(x) = 0\)
Giải các phương trình sau. π 1. 2sin( x − ) − 2 = 0 . 4 2. sin 2 x − 2 3 sin 2 x − cos x + 3 sin x = 0 .
giúp em với adim
lớp 11
Giải phương trình \(f'\left(x\right)=0\) biết rằng :
a) \(f\left(x\right)=3x+\dfrac{60}{x}-\dfrac{64}{x^3}+5\)
b) \(f\left(x\right)=\dfrac{\sin3x}{3}+\cos x-\sqrt{3}\left(\sin x+\dfrac{\cos3x}{3}\right)\)
Cho f(x)
log
5
(
sin
x
)
,
x
∈
(
0
;
π
/
2
)
. Tính f(x)
Đọc tiếp
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
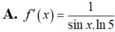
![]()
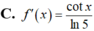
![]()






