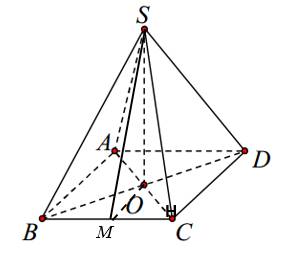
Cho hình chóp tứ giác
S
.
A
B
C
D
có đáy
A
B
C
D
là hình chữ nhật cạnh
A
B
=
a
,
A
D
=
a
2
, cạnh bên
S
A
vuông góc với mặt phẳng
A
B
C
D
, góc giữa
S
C
và mặt phẳng
A
B
C
D
bằng
60
0
. Gọi
M
là trung điểm của cạnh
S
B
(tham khảo hình vẽ). Khoảng cách từ điểm
M
tới mặt phẳng
A
B
C
D
bằng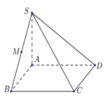
A. a 2 .
B. 3 a 2 .
C. 2 a 3 .
D. a 3 .