Cho hai đường thẳng song song Δ 1 và ∆ 2 . Nếu trên hai đường thẳng Δ 1 và ∆ 2 có tất cả 2018 điểm thì số tam giác lớn nhất có thể tạo ra từ 2018 điểm này là
A. 1020133294.
B. 1026225648.
C. 1023176448.
D. 1029280900.
Trong các mệnh đề sau đây mệnh đề nào là đúng?
a) Đường thẳng Δ là đường vuông góc chung của hai đường thẳng a và b nếu Δ ⊥a và Δ ⊥b.
b) Gọi (P) là mặt phẳng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với (P).
c) Gọi Δ là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì Δ là giao tuyến của hai mặt phẳng (a, Δ) và (b, Δ).
d) Cho hai đường thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Đường vuông góc chung Δ của hai đường thẳng chéo nhau a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.
Trong không gian Oxyz, cho đường thẳng Δ là giao tuyến của hai mặt phẳng (P):x+my-mz+1 = 0; (Q):mx+y+z+m=0. Đường thẳng Δ ′ qua gốc toạ độ O và song song với đường thẳng Δ . Ba điểm A,B,C lần lượt di động trên Oz, Δ , Δ ′. Giá trị nhỏ nhất của AB+BC+CA bằng
A. 1.
B. 2 2
C. 2.
D. 2
cho đường thẳng (d) : x - 2y + 1 = 0. nếu đường thẳng (Δ) đi qua M(1;-1) và song song với (d) thì (Δ) có phương trình ?
\(\Delta\) đi qua M(1,-1) có hệ số góc k
=> \(\Delta:y=k\left(x-1\right)-1=kx-k-1\)
\(\Delta\) song song d: \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) \(=>k=\dfrac{1}{2}\)
\(\Delta:y=\dfrac{1}{2}x-\dfrac{3}{2}\)
Trong không gian Oxyz, cho đường thẳng d: x = 1 + t, y = 2 -2t, z = -3. Viết phương trình tham số của đường thẳng Δ nằm trong mặt phẳng (Oxy), song song với d sao cho khoảng cách giữa hai đường thẳng d và Δ đạt giá trị nhỏ nhất
A. d: x = 1 + t, y = 2 -2t, z = 0
B. d: x = 1 + t, y = -2t, z = -3
C. d: x = t, y = 2 - 2t, z = -3
D. d: x = 1, y = 2, z = -3 + t
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 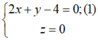
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 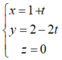
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Cho hai đường thẳng: Δ:(m+3)x+3y−2m+3=0,Δ′:2x+2y+2−3m=0. Tìm giá trị của tham số m để:
a, Đường thẳng △ song song với △'
b, Đường thẳng △ cắt đường thẳng △'
a.
Hai đường thẳng song song khi:
\(\dfrac{m+3}{2}=\dfrac{3}{2}\ne\dfrac{-2m+3}{2-3m}\)
\(\Leftrightarrow m=0\)
b.
Hai đường thẳng trùng nhau khi: \(\dfrac{m+3}{2}=\dfrac{3}{2}=\dfrac{-2m+3}{2-3m}\Rightarrow\) ko tồn tại m thỏa mãn
Vậy 2 đường thẳng cắt nhau khi \(m\ne0\)
Lập phương trình thanh số, phương trình tổng quát của đường thẳng Δ biết: d. Δ đi qua D(2; 5) và E(3; 1)
e. Δ đi qua G(2; 5) và song song với đường thẳng d: 2x-3y-3 = 0
g. Δ đi qua H(2; 5) và vuông góc với đường thẳng d: x + 3y + 2 = 0
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 2 và hai đường thẳng d: x - 2 1 = y 2 = z - 1 - 1 ,Δ: x 1 = y 1 = z - 1 - 1 . Phương trình nào dưới đây là phương trình mặt phẳng tiếp xúc với (S) và song song với d và Δ
A. y+z+3 = 0.
B. x+y+1 = 0.
C. x+z-1 = 0.
D. x+z+1 = 0
Trong không gian Oxyz, viết phương trình đường thẳng Δ song song với trục Oz và cắt hai đường thẳng d : x 1 = y − 1 2 = z − 6 3 ; d ' : x - 1 1 = y + 2 1 = z − 3 - 1 .
A. Δ : x = 2 y = 5 z = 12 + t
B. Δ : x = - 2 y = - 5 z = 12 + t
C. Δ : x = − 4 y = − 7 z = − 6 + t
D. Δ : x = 4 y = 7 z = − 6 + t
Trong mặt phẳng tọa độ Oxy, cho điểm K(1;1) và đường thẳng (Δ) có phương trình \(y=2x+\sqrt{3}\). Gọi (d) là 1 đường thẳng song song với đường thẳng (Δ) có và cắt trục tung tại điểm có tung độ bằng 1. Hãy tính khoảng cách từ K đến đường thẳng (d)
Gọi \(\left(d\right):y=ax+b\) là đt của (d)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne\sqrt{3}\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\Leftrightarrow2x-y+1=0\)
Khoảng cách từ K đến (d) là \(d\left(K;d\right)=\dfrac{6\cdot1-1+1}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)