Cho hình vuông ABCD có bốn đỉnh nằm trên đường tròn (O;\(3\sqrt{2}\)cm) Diện tích của hình vuông ABCD là
TC
Những câu hỏi liên quan
Cho đường tròn tâm O,bán kính 1,5cm.Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ
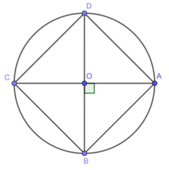
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông
Đúng 0
Bình luận (0)
Bài 7: Cho hình vuông ABCD có bốn đỉnh nằm trên hình tròn tâm O, bán kính 3cm. Tìm tỉ số phần trăm của diện tích hình tròn và diện tích hình vuông đó
Đọc tiếp
Bài 7: Cho hình vuông ABCD có bốn đỉnh nằm trên hình tròn tâm O, bán kính 3cm. Tìm tỉ số phần trăm của diện tích hình tròn và diện tích hình vuông đó
Diện tích hình tròn là:
3 x 3 x 3,14 = 28,26 ( cm² )
Độ dài đường chéo AC là:
3 x 2 = 6 (cm)
Diện tích hình vuông là:
6 x 6 = 36 ( cm² )
Tỉ số phần trăm của diện tích hình tròn và diện tích hình vuông là:
28,26 : 36 x 100% = 78,5%
Đáp số: 78,5%
Đúng 5
Bình luận (1)
Cho hình vuông ABCD. Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó
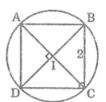
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a. a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn. b) Xác định tâm và bán kính của đường tròn đó.
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng nằm trên một đường tròn
b: Tâm là trung điểm của AC
Đúng 0
Bình luận (0)
Bài 1.3: Cho hình vuông ABCD cạnh a.
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn.
b) Xác định tâm và bán kính của đường tròn đó.
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
\(R=\dfrac{AC}{2}\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính 1,5 cm. Hãy vẽ hình vuông ABCD có 4 đỉnh nằm trên đường tròn đó. Nêu cách vẽ ?
Cho hình vuông ABCD cạnh a. a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn. b) Xác định tâm và bán kính của đường tròn đó.
giúp mk với mk đang cần gấp
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
b: Tâm là trung điểm của AC
Bán kính là \(\dfrac{a\sqrt{2}}{2}\)
Đúng 1
Bình luận (0)
Cho hình vuông ABCD
a) Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó ?
b) Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2 dm ?
cho tứ giác ABCD có bốn đỉnh A, B, C, D nằm trên đường tròn (O;R) có AB vuông góc với BD. kẻ đường kính CE.
c/m AB^2 +CD^2 +BC^2 +AD^2= 8R^2






