Cho hàm số f(x)= l n 2 ( x 2 - 2 x + 4 ) . Tìm các giá trị của x để f'(x)>0
A. x ≠ 0
B. x> 0
C. x> 1
D. ∀ x
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Cho hàm số f(x) = mx^2 +2x +2 khi x>0 và nx +2 khi x<=0. Tìm tất cả các giá trị của các tham số m,n sao cho f(x) có đạo hàm tại x=0
Để hàm số có đạo hàm tại x=0 phải thỏa mãn 2 điều kiện, đó là hàm số liên tục tại x=0 và có đạo hàm bên trái bằng đạo hàm bên phải
Để hàm số liên tục tại x=0 \(\Leftrightarrow\lim\limits_{x\rightarrow0^+}=\lim\limits_{x\rightarrow0^-}=f\left(0\right)\Leftrightarrow2=2\left(tm\right)\)
\(f'\left(0^+\right)=\lim\limits_{x\rightarrow0^+}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^+}\dfrac{mx^2+2x+2-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(mx+2\right)}{x}=2\)
\(f'\left(0^-\right)=\lim\limits_{x\rightarrow0^-}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^-}\dfrac{nx+2-2}{x}=n\)
\(\Rightarrow\left\{{}\begin{matrix}m\in R\\n=2\end{matrix}\right.\)
\(f\left(0^+\right)=f\left(0^-\right)\Leftrightarrow n=2\)
Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số \(m\) để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\).
, ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >, ( )
Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số f(x) = x2 -1 . Tìm các giá trị của x sao cho f(1-x) nhận giá trị âm
cho hàm số f(x)=\(\begin{cases} \sqrt{2x-4}+3 \\ \dfrac{x+2}{x^2-2mx+m^2+2} \end{cases} \)(trên) khi x≥2, (dưới) khi x<2. Tìm các giá trị của tham số thực m để hàm số liên tục trên R
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\sqrt{2x-4}+3\)
\(=\sqrt{2\cdot2-4}+3=3\)
\(f\left(2\right)=\sqrt{2\cdot2-4}+3=0+3=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x+2}{x^2-2mx+m^2+2}\)
\(=\dfrac{2+2}{2^2-2m\cdot2+m^2+2}=\dfrac{4}{m^2-4m+6}\)
Để hàm số f(x) liên tục trên R thì f(x) liên tục tại x=2
=>\(\dfrac{4}{m^2-4m+6}=3\)
=>\(4=3\left(m^2-4m+6\right)\)
=>\(3m^2-12m+18-4=0\)
=>\(3m^2-12m+14=0\)
\(\Leftrightarrow3m^2-12m+12+2=0\)
=>\(3\left(m-2\right)^2+2=0\)(vô lý)
=>\(m\in\varnothing\)
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
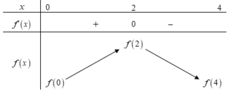
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Cho hàm số sau: y = f(x) = ( x2 - 2( m + 4) x + 2m + 12).ex. Tìm tổng các giá trị nguyên của m để hàm số nghịch biến trên TXĐ là S thì giá trị của S sẽ là:
A. 15
B. -12
C. -15
D. -10
Chọn C.
+) TXĐ: D = R
+) Ta có đạo hàm y’ = ( x2 - 2( m + 3) x + 4) .ex .
Hàm số nghịch biến trên TXĐ khi y’ = ( x2 - 2( m + 3) x + 4) .ex ≤ 0 mọi x

cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
tick rồi mk giải chi tiết cho
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0