Chọn A

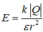
E N / E M =9/25=> r N / r M =5/3

A M = r M = r N - M N = 3 r N / 5 E N / E M

r N =MN=20=> r N =50cm=>AM=30cm=0,3m

a: Để M là số nguyên thì 5 chia hết cho căn a+1

=>căn a+1 thuộc {1;5}

=>a thuộc {0;4}

b: Khi a=4/9 thì \(M=1+\dfrac{5}{\dfrac{2}{3}+1}=1+5:\dfrac{5}{3}=1+3=4\)

=>M là số nguyên

c: \(\sqrt{a}+1>=1\)

=>\(\dfrac{5}{\sqrt{a}+1}< =5\)

=>M<=6

\(1< =\dfrac{5}{\sqrt{a}+1}< =5\)

=>2<=M<=6

M=2 khi \(\dfrac{5}{\sqrt{a}+1}+1=2\)

=>\(\dfrac{5}{\sqrt{a}+1}=1\)

=>căn a+1=5

=>căn a=4

=>a=16

M=3 khi \(\dfrac{5}{\sqrt{a}+1}=2\)

=>căn a+1=5/2

=>căn a=3/2

=>a=9/4

M=4 thì \(\dfrac{5}{\sqrt{a}+1}=3\)

=>căn a+1=5/3

=>căn a=2/3

=>a=4/9

\(M=5\Leftrightarrow\dfrac{5}{\sqrt{a}+1}=4\)

=>căn a+1=5/4

=>căn a=1/4

=>a=1/16

\(3,\\ a,=a^2+2a+1-a^2+2a-1-3a^2+3=-3a^2+4a+3\\ b,=\left(m^3-m+1-m^2+3\right)^2=\left(m^3-m^2-m+4\right)^2\\ 4,\\ a,\Leftrightarrow25x^2+10x+1-25x^2+9=3\\ \Leftrightarrow10x=-7\Leftrightarrow x=-\dfrac{7}{10}\\ b,\Leftrightarrow-9x^2+30x-25+9x^2+18x+9=30\\ \Leftrightarrow48x=46\Leftrightarrow x=\dfrac{23}{24}\\ c,\Leftrightarrow x^2+8x+16-x^2+1=16\\ \Leftrightarrow8x=-1\Leftrightarrow x=-\dfrac{1}{8}\)

a, Ta có : M= 1 - 2 + 3 -4 + 5-6 +... + 19 - 20

                   = ( 1-2 ) + ( 3 - 4 ) + ( 5-6 ) + ...+ ( 19 - 20 )

                   = ( -1 ) + ( -1 )  + ( -1 ) +...+ (-1 )  ( có 10 số  ( - 1 )

                    = 10 . (-1 )

câu b làm sao vậy bạn

b,  Đặt S= 13 - 12 + 11 + 10 - 9 + 8 - 7 - 6 + 5 - 4 + 3 + 2 -1

     Ta có : S= 13  - 12 + 11 + 10 - 9 + 8 - 7 - 6 + 5 - 4 + 3 + 2 -1

                   = 13 - ( 12 - 11 - 10 + 9 ) + ( 8 - 7 - 6 + 5 ) - ( 4 - 3 - 2 + 1 )

                   = 13 - 0 + 0 - 0

                    = 13

Hàm số bị viết thiếu `y=`   !

Đk: `-2 <= m <= 2`

Để h/s đồng biến `=>\sqrt{4-m^2}/[9-m^2] > 0`   với `-2 < m < 2`

    `=>9-m^2 > 0`

 `<=>(3-m)(3+m) > 0<=>(m-3)(m+3) < 0<=>-3 < m < 3`

  Kết hợp đk

 `=>-2 < m < 2`

 `->bb C`

Chọn B

B

B

\(\dfrac{5}{11}=\dfrac{m}{44}\)

Thay m=20

=>B