Cho hàm số f ( x ) = x 4 + 2 m x 2 + m với m làm tham số, m>0
Đặt g ( x ) = f ( x ) + f ' ( x ) + f ' ' ( x ) + f ( 3 ) ( x ) + f ( 4 ) ( x ) Mệnh đề nào dưới đây đúng
A. g ( x ) ≥ 0 ∀ x
B. g ( x ) < 0 ∀ x
C. g ( x ) > 0 ∀ x
D. g ( x ) ≤ 0 ∀ x
1/ Cho hàm số \(f\)(\(x\))=\(\dfrac{1}{3}\)\(x\)\(^3\)+\(x \)\(^2\)-(\(m\)+1)\(x\)-\(m\)+3. Với \(m\) là tham số. Có bao nhiêu số nguyên \(m\) thuộc đoạn [-10;10] để \(f\)'(\(x\)) ≥ 0, ∀\(x\) ϵ \(R\)
2/ Cho hàm số \(y\) = \(\dfrac{mx+4}{x+m}\). Với \(m\) là tham số. Có bao nhiêu số nguyên m thuộc đoạn [-5;2023] để \(y\)' > 0, ∀\(x\) ϵ (0;+∞).
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
cho hàm số y=f(x)=(x+4)|x+2| tìm m để hàm số y=f(x) cắt đường thẳng y=m tại 3 điểm phân biệt
cho hàm số \(f\left(x\right)=x^4-\left(m^2-3x+2\right)x^3+2x^2-\left(m-1\right)x+1\)
tìm m để hàm số chẵn
Coi lại đề, cái ngoặc thứ 2 ấy, \(m^2-3x+2\) là có vấn đề rồi
Cho hàm số y = f(x) liên tục trên R sao cho m a x x ∈ 0 ; 10 f ( x ) = f ( 2 ) = 4 . Xét hàm số g ( x ) = f ( x 3 + x ) − x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ 0 ; 2 g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
cho hàm số y= f(x)=(m+1)x. Tìm m để f(2)=4 . Vẽ đồ thị hàm số với m vừa tìm được
Thay x=2 vào hàm số f(x)=(m+1)x ta được (m+1).2
=> Để f(2)=4 thì m+1 = 4:2 = 2
<=> m = 2-1 = 1
cho hàm số f(x)= (m-1)x4+ (m2-27)x3+(m2-1)x2 +(m2-9)x+(m2-9) (m2-1)
a, tìm m để f(x) là hàm lẻ
b, tìm m để f(x) là hàm chẵn
Cho hàm số
y = f(x) = (4 - m^2)x^2 - (2m + 1)x+3
Tìm m để hàm số luôn đồng biến trên tập số thực R
Cho hàm số y = f(x) liên tục trên ℝ sao cho m a x x ∈ [ 0 ; 10 ] f ( x ) = f(2) = 4. Xét hàm số g(x) = f x 3 + x - x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ [ 0 ; 2 ] g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Chọn D
Xét hàm số ![]()
![]()
Ta có ![]() nên
nên ![]()
Vì vậy ![]() khi t = 2
⇔
x = 1
khi t = 2
⇔
x = 1
Mặt khác ![]()
![]() Suy ra
Suy ra ![]() khi x = 1
khi x = 1
Vậy ![]() ⇔
m = 3
⇔
m = 3
Cách 2: Tác giả: Nguyễn Trọn g Lễ; Fb: Nguyễn Trọng Lễ.
Phương pháp trắc nghiệm
Chọn hàm y = f(x) = 4 thỏa mãn giả thiết: hàm số y = f(x) liên tục trên ℝ có
![]()
Ta có ![]()
![]()
![]()
Xét hàm số g(x) liên tục trên đoạn [0;2], g'(x) = 0 ⇔ x = 1. Ta có g(0) = 4 + m, g(1) = 5 + m, g(2) = 4 + m
Rõ ràng g(0) = g(2) < g(1) nên ![]()
Vậy 5 + m = 8 => m = 3
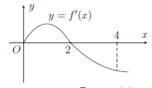
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
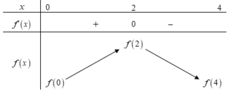
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
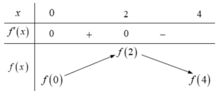
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()