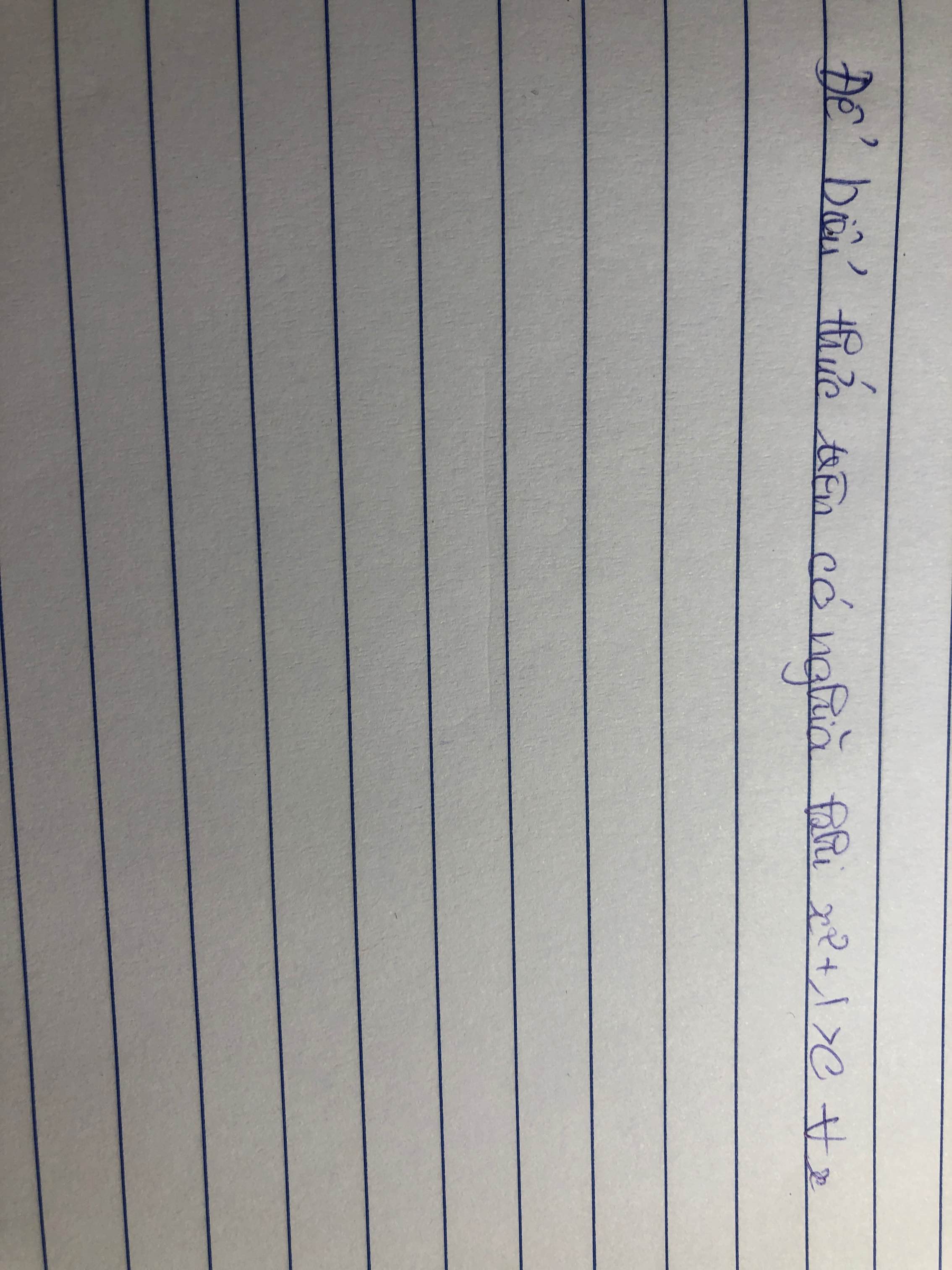Tìm giá trị x để biểu thức sau có nghĩa :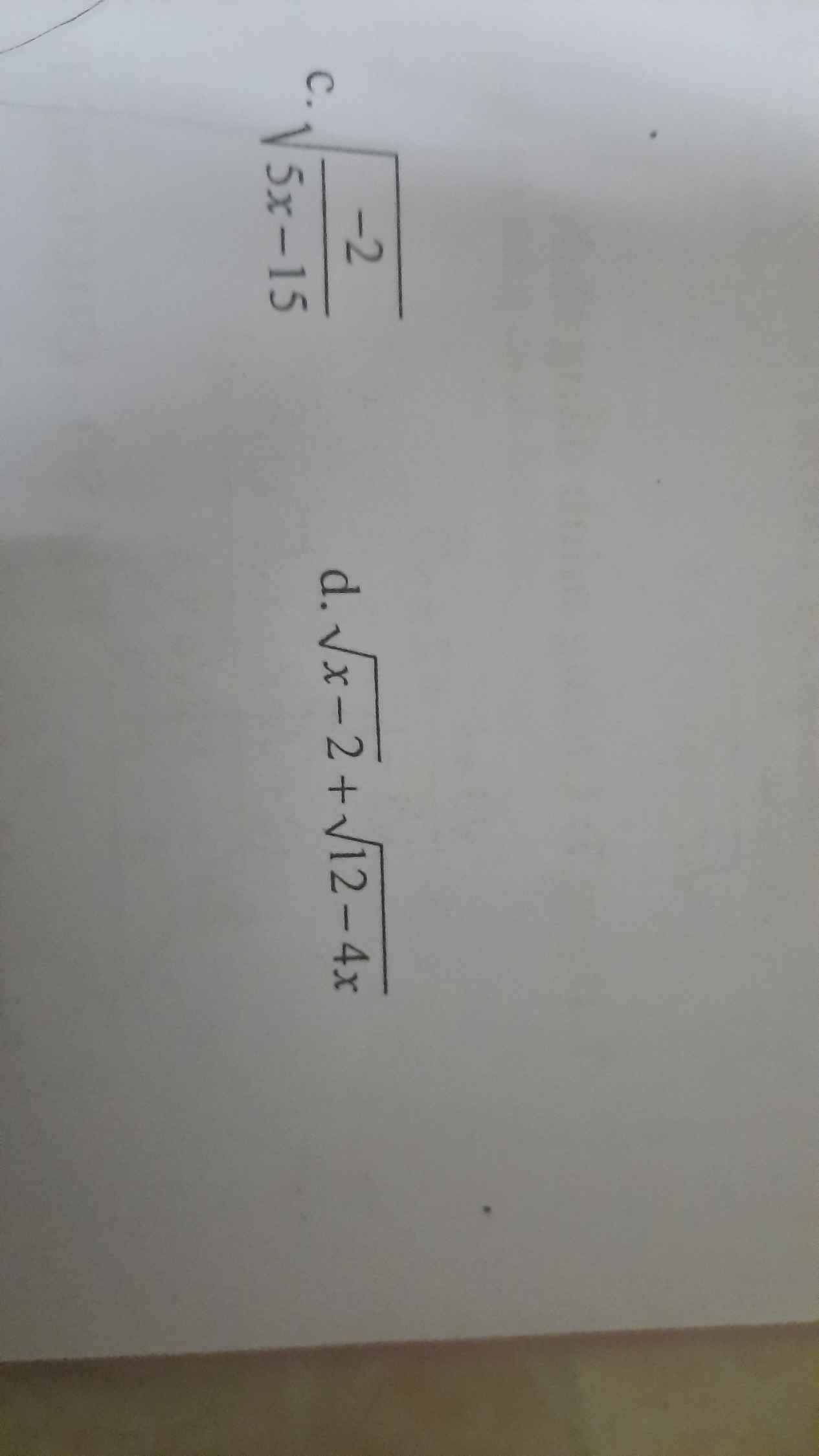
TT
Những câu hỏi liên quan
Tìm các giá trị của x để biểu thức sau có nghĩa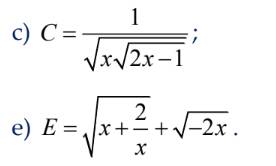
c
Để biểu thức C có nghĩa thì
\(\sqrt{x\sqrt{2x-1}}>0\)
<=> \(\left\{{}\begin{matrix}x>0\\2x-1>0\Leftrightarrow x>\dfrac{1}{2}\end{matrix}\right.\Rightarrow x>\dfrac{1}{2}\)
Vậy để biểu thức C có nghĩa thì \(x>\dfrac{1}{2}\)
Giải câu e:
Điều kiện để biểu thức E có nghĩa:
\(\left\{{}\begin{matrix}x+\dfrac{2}{x}\ge0\\-2x\ge0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}\dfrac{x^2+2}{x}\ge0\\x\le0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x>0\\x\le0\end{matrix}\right.\)
Vậy không tồn tại x để biểu thức E có nghĩa.
Đúng 1
Bình luận (2)
Tìm các giá trị của x để các biểu thức sau có nghĩa
√x+2 + √3-x
<=> x + 2 ≥ 0 và 3 - x ≥ 0
<=> x ≥ -2 và x ≤ 3
vậy -2 ≤ x ≤ 3
Đúng 0
Bình luận (0)
cho biểu thức C= x/2x-2 + x^2+1/2-2x^2
a) Tìm x để biểu thức C có nghĩa
b) Rút gọn biểu thức C*c.
c)Tìm giá trị của x để biểu thức có giá trị -0,5
cho biểu thuiwcs C= x/2x-2 + x^2+1/2-2x^2
a) tìm x để biểu thức C có nghĩa
b) rút gọn biểu thức ÙC
c) tìm giá trị của x để giá trị biểu thức C= -1/2
cho biểu thức C=x/2x-2+2x^2+1
a. tìm x để biểu thức C có nghĩa
b. rút gọn biểu thức C
c. tìm giá trị của x để biểu thức có giá trị -0,5
Bài 1 (2điểm)1) Nêu điều kiện để √a có nghĩa ?2) Áp dụng: Tìm x để các căn thức sau có nghĩa:Bài 2: ( 3 điểm ): Rút gọn biểu thứcBài 3 ( 4 điểm ) Cho biểu thức(Với x 0; x 1; x4)a/ Rút gọn P.b/ Với giá trị nào của x thì P có giá trị bằng 1/4c/ Tính giá trị của P tại x 4 + 2√3d/ Tìm số nguyên x để biểu thức P có giá trị là số nguyên ?Bài 4 : ( 1 điểm ): ChoTìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Đọc tiếp
Bài 1 (2điểm)
1) Nêu điều kiện để √a có nghĩa ?
2) Áp dụng: Tìm x để các căn thức sau có nghĩa:
![]()
Bài 2: ( 3 điểm ): Rút gọn biểu thức

Bài 3 ( 4 điểm ) Cho biểu thức
 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)
a/ Rút gọn P.
b/ Với giá trị nào của x thì P có giá trị bằng 1/4
c/ Tính giá trị của P tại x = 4 + 2√3
d/ Tìm số nguyên x để biểu thức P có giá trị là số nguyên ?
Bài 4 : ( 1 điểm ): Cho
![]()
Tìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
TÌM SỐ NGUYÊN X ĐỂ BIỂU THỨC SAU ĐẠT GIÁ TRỊ NHỎ NHẤT. TÍNH GIÁ TRỊ ĐÓ
A=[2x+6]+1
[ ] có nghĩa là GIÁ TRỊ TUYỆT ĐỐI nha các bạn
ta có: [2x+6] luôn luôn dương
<=> [2x+6] +1 >= 1
=> giá trị nhở nhất = 1 tại x bằng -3
Đúng 0
Bình luận (0)
Tìm giá trị của x để biểu thức có nghĩa
\(\sqrt{x^2+1}\)
thấy \(x^2+1\ge1>0\left(\forall x\right)\)
nên \(\sqrt{x^2+1}\) luôn xác định với mọi x
Đúng 1
Bình luận (0)
Cho biểu thức A=\(\dfrac{x\sqrt{x}-4x-\sqrt{x}+4}{2x\sqrt{x}-14x+28\sqrt{x}-16}\)
a/ Tìm x để A có nghĩa, từ đó rút gọn A.
b/ Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên
Lời giải:
a.
\(A=\frac{(x\sqrt{x}-4x)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
ĐKXĐ: \(\left\{\begin{matrix} x\geq 0\\ \sqrt{x}-4\neq 0\\ \sqrt{x}-2\neq 0\\ \sqrt{x}-1\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ x\neq 16\\ x\neq 4\\ x\neq 1\end{matrix}\right.\)
\(A=\frac{x(\sqrt{x}-4)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{2}-2)(\sqrt{x}-1)}=\frac{(x-1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
\(=\frac{(\sqrt{x}-1)(\sqrt{x}+1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}=\frac{\sqrt{x}+1}{2(\sqrt{x}-2)}\)
b.
Với $x$ nguyên, để $A\in\mathbb{Z}$ thì $\sqrt{x}+1\vdots 2(\sqrt{x}-2)}$
$\Rightarrow \sqrt{x}+1\vdots \sqrt{x}-2$
$\Leftrightarrow \sqrt{x}-2+3\vdots \sqrt{x}-2$
$\Leftrightarrow 3\vdots \sqrt{x}-2$
$\Rightarrow \sqrt{x}-2\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow x\in\left\{1;9;25\right\}$
Thử lại thấy đều thỏa mãn.
Đúng 1
Bình luận (0)