Tập nghiệm S của bất phương trình log 2 x + 2 ≤ 0 là
A. S = 0 ; - 1
B. S = - 1 ; + ∞
C. S = - 2 ; - 1
D. S = - 2 ; + ∞
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x 0 . Giá trị của a + b - x 0 bằng:
A. 100
B. 30
C. 150
D. 50
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = (a;b)\{x0}. Giá trị của a + b – x0 bằng:
A. 100
B. 30
C. 150
D. 50
Đáp án D.
Phương pháp: ![]()
Cách giải: ĐK: ![]()
![]()
![]()
![]()
![]()
![]()
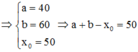
Tập nghiệm của bất phương trình 5 - 2x >= 0 là :
A. S = {x/x>=5 phần 2}
B. S = {x/x<=5 phần 2}
C. S = {x/x>=-5 phần 2} |
\(5-2x\ge0\)
\(\Leftrightarrow5\ge2x\)
\(\Leftrightarrow x\le\dfrac{5}{2}\)
\(S=\left\{x|x\le\dfrac{5}{2}\right\}\)
=> B
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình \(\left|x+1\right|\)<x là:
A. \(S=\left(\dfrac{1}{2};+\infty\right)\) B. \(S=\left(0;\dfrac{1}{2}\right)\) C. \(S=\varnothing\) D. \(S=\left(-\infty;-\dfrac{1}{2}\right)\)
Biết tập nghiệm S của bất phương trình log π 6 log 3 x - 2 > 0 là khoảng (a;b). Tính b – a.
A. 2
B. 4
C. 3
D. 5
Biết tập nghiệm S của bất phương trình log π 6 log 3 x - 2 > 0 là khoảng (a;b). Tính b - a.
A. 2
B. 4
C. 3
D. 5
Đáp án A.
Ta có: log π 6 log 3 x - 2 > 0 ⇔ 0 < log 3 x - 2 < 1 ⇔ x - 2 > 1 x - 2 < 3 ⇔ 3 < x < 5
Vậy S = 3 ; 5 ⇒ b - a = 2 .
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)