Đáp án D.
Phương pháp: ![]()
Cách giải: ĐK: ![]()
![]()
![]()
![]()
![]()
![]()
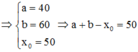
Đáp án D.
Phương pháp: ![]()
Cách giải: ĐK: ![]()
![]()
![]()
![]()
![]()
![]()
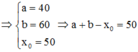
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Gọi S là tập tất cả các giá trị thực của tham số m để bất phương trình
x 6 + 3 x 4 − m 3 x 3 + 4 x 2 − m x + 2 ≥ 0 có nghiệm với mọi x ∈ ℝ . Biết rằng S = a ; b , a , b ∈ ℝ . Tính P = 2 b − 3 a
A. P = 5
B. P = 10
C. P = 15
D. P = 0
Tập nghiệm của bất phương trình 2 . 7 x + 2 + 7 . 2 x + 2 ≤ 351 14 x có dạng S = [a;b]. Giá trị b - 2a thuộc khoảng nào sau đây?
A. 3 ; 10
B. (-4;2)
C. 7 ; 4 10
D. 2 9 ; 49 5
Tập nghiệm của bất phương trình 3 . 9 x - 10 . 3 x + 3 ≤ 0 có dạng S = [ a;b ]. Tính giá trị của b - a
A. 1
B. 3 2
C. 2
D. 5 2
Tập nghiệm của bất phương trình 3 . 9 x - 10 . 3 x + 3 ≤ 0 có dạng S = a ; b trong đó a, b là các số nguyên. Giá trị của biểu thức 5 b - 2 a bằng
A. 7
B. 43 3
C. 3
D. 8 3
Gọi S là tập nghiệm của bất phương trình 2 x 3 + x ≤ x + 2 2 x + 5 . Biết S = a ; b , a , b ∈ ℝ . Giá trị M = a 2 b 3 của gần nhất với số nào sau đây:
A. 0,12
B. 2,42
C. 2,12
D. 1,12
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x 1 , x 2 thỏa x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Cho hàm số y = f x = 2 x 2 − 7 x + 6 x − 2 k h i x < 2 a + 1 − x 2 + x k h i x ≥ 2 . Biết a là giá trị để hàm số f(x) liên tục tại x 0 = 2 , tìm nghiệm nguyên của bất phương trình − x 2 + a x + 7 4 > 0 .
A. 1
B. 4
C. 3
D. 2
Tập nghiệm của bất phương trình: 2 . 4 x - 5 . 2 x + 2 ≤ 0 có dạng S = a ; b Tính b - a
A. 1
B. 5 2
C. 2
D. 3 2