Tính diện tích toàn phần (tổng diện tích các mặt) của khối hai mươi mặt đều cạnh a.
PB
Những câu hỏi liên quan
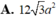
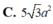
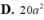
một khối rubik có dạng hình chóp tam giác đêuuf( các mặt khối rubik là các tam giác đều bằng nhau ) chu vi đáy bằng 234mm, đường cao của mặt bên hình chóp là 67,5mm
a) tính diện tích xung quanh, diện tích toàn phần (tổng diện tích các mặt của rubik đó)
b) biết chiều cao của khối rubik là 63,7mm. tính thể tích của khối rubik đó
cho hình chóp tứ giác đều có cạnh đáy 8cm, trung đoạn bằng 5cm. Tính diện tích xung quanh và diện tích toàn phần ( tổng diện tích các mặt của hình chóp ) của hình tứ giác đều đó ?
Nữa chu vi đáy của hình chóp đều:
\(8\cdot4:2=16\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=16\cdot5=80\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(S_đ=8^2=64\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=64+80=144\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Sxq=1/2*8*4*5=80cm2
Stp=80+8^2=144cm2
Đúng 0
Bình luận (0)
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .
A
.
2
a
3
3
B
.
a
3
3
16
C
.
8
a
2
3
D
.
8...
Đọc tiếp
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .
A . 2 a 3 3
B . a 3 3 16
C . 8 a 2 3
D . 8 a 2
Đáp án C
Diện tích của tam giác đều có cạnh là a bằng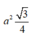 
Ta có: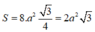 
Đúng 0
Bình luận (0)
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a A.
8
a
2
B.
2
a
2
3
C.
8
a
2
3
D.
a
2
3
16
Đọc tiếp
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a
A. 8 a 2
B. 2 a 2 3
C. 8 a 2 3
D. a 2 3 16
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a . A.
2
a
2
3
.
B.
a
2
3
16
.
C.
8
a
2
3
.
D.
8
a
2
.
Đọc tiếp
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .
A. 2 a 2 3 .
B. a 2 3 16 .
C. 8 a 2 3 .
D. 8 a 2 .
Đáp án C
Diện tích của tam giác đều có cạnh là a bằng a 2 3 4 Ta có S = 8. a 2 3 4 = 2 a 2 3
Đúng 0
Bình luận (0)
Tính tổng diện tích các mặt của một khối bát diện đều cạnh
a
.
A.
8
a
2
.
B.
2
a
2
3
.
C.
8
a
2
3
.
D.
a
2...
Đọc tiếp
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .
A. 8 a 2 .
B. 2 a 2 3 .
C. 8 a 2 3 .
D. a 2 3 16 .
Đáp án B.
Bát diện đều có 8 mặt đều là tam giác đều có cạnh a.
Diện tích tam giác đều có cạnh a là S = 1 2 a . a . sin 60 ^ = 3 4 a 2 ⇒ Tổng diện tích các mặt của khối bát diện đều là 8. 3 4 a 2 = 2 3 a 2 .
Đúng 0
Bình luận (0)
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu). A.
2
a
2
3...
Đọc tiếp
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu).
A. 2 a 2 3
B. a 2 2 3
C. a 2 4
D. a 2 4 3
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu). A.
2
a
2
3...
Đọc tiếp
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu).
A. 2 a 2 3
B. a 2 2 3
C. a 2 4
D. a 2 4 3
một hình chóp tứ giác đều có chiều cao bằng 15cm, trung đoạn bằng 17cm, độ dài cạnh đáy của hình chóp bằng 16cm. Tính diện tích xung quanh, diện tích toàn phần ( tổng diện tích các mặt đáy của hình chóp ), thể tích của hình chóp tứ giác đều?
Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Đúng 0
Bình luận (0)
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)
Đúng 0
Bình luận (0)