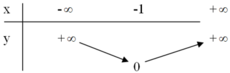
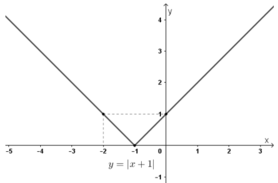
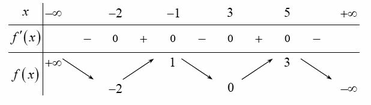
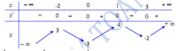
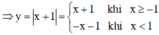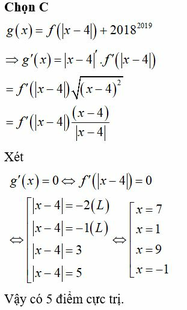Xét chiều biến thiên của hàm số
y = x 2 + 8 x - 24 x 2 - 4
A. Hàm số nghịch biến trên mỗi khoảng - ∞ ; - 2 ; - 2 ; 1 ; 4 ; + ∞ và đồng biến trên mỗi khoảng ( 1;2 ); ( 2;4 )
B. Hàm số đồng biến trên mỗi khoảng - ∞ ; - 2 ; - 2 ; 1 ; 4 ; + ∞ và nghịch biến trên mỗi khoảng ( 1;2 ); ( 2;4 )
C. Hàm số đồng biến trên mỗi khoảng - ∞ ; - 2 ; - 2 ; 1 và nghịch biến trên mỗi khoảng ( 1;2 ); ( 2;4 ); 4 ; + ∞
D. Hàm số nghịch biến trên mỗi khoảng - ∞ ; - 2 ; - 2 ; 1 và đồng biến trên mỗi khoảng ( 1;2 ); ( 2;4 ); 4 ; + ∞