Giả sử đồ thị (C) của hàm số y = 2 x ln 2 cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB.
A. S = 1 ln 2
B. S = 1 ln 2 2
C. S = 1 ln 2 3
D. S = 1 ln 2 4
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là (C).Giả sử (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2, đồng thời (d) cắt đồ thị (C) tại N, tìm tọa độ N.
A. N(1;-1)
B. N(2;3)
C. N(-4;-51)
D. N(3;19)
- Tiếp tuyến (d) tại điểm M của đồ thị (C) có hoành độ x 0 = 0 ⇒ y 0 = 3 .
- Ta có:
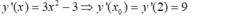
- Phương trình tiếp tuyến (d) tại điểm M của đồ thị (C) là:
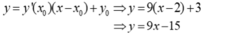
- Xét phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm phương trình :
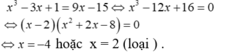
- Với x = -4 thì y = 9.(-4) – 15 = -51.
- Vậy N(- 4 ; -51) là điểm cần tìm.
Chọn C.
Cho hàm số: y = x3 - 3x2 + 2 (C)
Giả sử A(x0,y0) ∈ (C), tiếp tuyến tại A cắt đồ thị hàm số tại B. Tìm tọa độ B the x0
Trước hết chúng ta cần nói sơ đến định lý Viet cho pt bậc 3:
Pt bậc 3 có dạng \(ax^3+bx^2+cx+d=0\) có 3 nghiệm \(x_1;x_2;x_3\) thì:
\(x_1+x_2+x_3=-\dfrac{b}{a}\)
Giả sử tọa độ B có dạng \(B\left(x_B;y_B\right)\) và pt đường thẳng d qua B có dạng:
\(y=ax+b\)
Pt hoành độ giao điểm d và (C):
\(x^3-3x^2+2=ax+b\)
\(\Leftrightarrow x^3-3x^2-ax+2-b=0\) (1)
Do d tiếp xúc (C) tại A (có hoành độ giao điểm là hoành độ của A bằng \(x_0\)) và cắt (C) tại B (có hoành độ giao điểm là hoành độ của B) nên \(x_0\) là nghiệm kép và \(x_B\) là nghiệm đơn của (1)
Hay nói cách khác, \(x_0;x_0;x_B\) là 3 nghiệm của (1)
Theo hệ thức Viet: \(x_0+x_0+x_B=3\Leftrightarrow x_B=3-2x_0\)
\(B\in\left(C\right)\Rightarrow y_B=\left(3-x_0\right)^3-3\left(3-x_0\right)^2+2=-x_0^3+6x_0^2-9x_0+2\)
Vậy tọa độ B có dạng: \(B\left(3-x_0;-x_0^3+6x_0^2-9x_0+2\right)\)
Câu 39:
Ta có: \(y'=\dfrac{-2-m}{\left(x-2\right)^2}\)
Phương trình đường thẳng d qua A có dạng: \(y=k\left(x-1\right)+2\)
Để d tiếp xúc (C) \(\Leftrightarrow\dfrac{x+m}{x-2}=k\left(x-1\right)+2\) có nghiệm kép
\(\Leftrightarrow kx^2-\left(3k-1\right)x+2k-m-4=0\)
\(\Delta=\left(3k-1\right)^2-4k\left(2k-m-4\right)=0\)
\(\Leftrightarrow k^2+2k\left(2m+5\right)+1=0\) (1)
Để có 2 tiếp tuyến thì (1) có 2 nghiệm pb \(\Leftrightarrow\Delta'=\left(2m+5\right)^2-1>0\)
Khi đó theo Viet: \(\left\{{}\begin{matrix}k_1+k_2=-2\left(2m+5\right)\\k_1k_2=1\end{matrix}\right.\)
Mặt khác tam giác ABC đều \(\Rightarrow\left(AB;AC\right)=60^0\)
\(\Leftrightarrow tan60^0=\left|\dfrac{k_1-k_2}{1+k_1k_2}\right|=\left|\dfrac{k_1-k_2}{2}\right|\)
\(\Rightarrow\left\{{}\begin{matrix}\left|k_1-k_2\right|=2\sqrt{3}\\k_1+k_2=-2\left(2m+5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(k_1+k_2\right)^2-4k_1k_2=12\\k_1+k_2=-2\left(2m+5\right)\end{matrix}\right.\)
\(\Leftrightarrow4\left(2m+5\right)^2-4=12\)
\(\Leftrightarrow...\)
Giả sử đồ thị (C) của hàm số y = ( 2 ) x ln 2 cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB
A. S = 1 ln 2
B. S = ( 1 ln 2 ) 2
C. S = ( 1 ln 2 ) 3
D. S = ( 1 ln 2 ) 4
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Oy xuống dưới 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Chọn A.
Theo lý thuyết, ta chọn câu A.
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là
A. (0;-1)
B. 5 2 ; 8
C. 0 ; - 1 v à 5 2 ; 9
D. 5 2 ; 9
f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
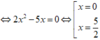
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là C , khi tịnh tiến C theo O y lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
![]()
![]()
![]()
![]()
Chọn A.
Đặt f ( x ) = x 4 - 2 x 2 - 1 thì khi tịnh tiến (C) theo O y lên trên 1 đơn vị thì sẽ được đồ thị của y = f ( x ) + 1 = x 4 - 2 x 2 .
C3: Giả sử các biểu thức đều có nghĩa. Với giá trị nào của a thì hai phân thức x/x+1 và ax^2-ax/x^2-1 bằng nhau:
A. -1 B. 1 C. 2 D.3
C5: Hàm số nào sau đây là hàm số bậc nhất
A. y=2x-1 B.y=2 C.y=x^2+x+1 D. y=2/x
C6: Đồ thị hàm số y=x+2 đi qua điểm có tọa độ nào sau đây
A. (0;-2) B.(1;3) C.(-1;0) D.(0;0)
C8: Giá trị m để đường thẳng y=(m-1)x+3 với ( m khác 1) song song với đường thẳng y=x là ?
A. m=0 B. m=1 C. m=2 D.không có giá trị của m
C9: Tổng số cạnh bên và cạnh đáy của hình chóp tam giác đều là
A.4 B.6 C.8 D.10
C10 S xung quanh hình chóp đều =?
A,tích nửa chu vi đáy và đường cao của hình chóp
B. Tích nửa chu vi đáy và độ dài trung đoạn
C. Tích chu vi đáy và độ dài trung đoạn
D. Tổng chu vi đáy và trung đoạn
C11 : Tứ giác ABCD có C=50 độ ; D=60 độ; A:B=3:2. Số đo B bằng?
A 50 độ B.100 độ C.150 độ D.200 độ
C12 :phát biểu nào sau đây là sai?
A. tứ giác có 4 cạnh =nhau và 4 góc = nhau là hình vuông
B. tứ giác có 2 dường chéo bằng nhau là hình bình hành
C. tứ giác có 4 cạnh bằng nhau là hình thoi
D. Tứ giác có 4 góc = nhau là hình chữ nhật
Câu 3: B
Câu 5: A
Câu 6: B
Câu 8: C
Câu 9: B
Câu 10:B
Câu 11: B
Câu 12: B