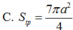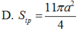Trong không gian Oxyz, cho hình thang cân ABCD có các đáy lần lượt là AB, CD. Biết A(3;1;-2), B(-1;3;2), C(-6;3;6), và D(a;b;c) với a, b, c ∈ ℝ . Tính T = a+ b+ c.
A. T = - 3
B. T = 1
C. T = 3
D. T = - 1
Trong không gian Oxyz, cho hình thang cân ABCD có các đáy lần lượt là AB, CD. Biết A ( 3 ; 1 ; - 2 ) , B ( - 1 ; 3 ; 2 ) , C ( - 6 ; 3 ; 6 ) và D ( a ; b ; c ) với . Tính T = a + b + c
A. - 3
B. 1
C. 3
D. - 1
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
Trong không gian cho hình thang cân ABCD có AB//CD, AB = a,CD = 2a,AD = a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
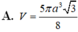
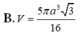
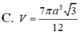
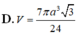
Trong không gian cho hình thang cân ABCD có AB//CD, AB=a, CD=2a, AD=a. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
A. V = 5 πa 3 3 8
B. V = 5 πa 3 3 16
C. V = 7 πa 3 3 12
D. V = 7 πa 3 3 12
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh S x q của khối K
A. S x q = πa 2 2
B. S x q = 3 πa 2 2
C. S x q = 3 πa 2
D. S x q = πa 2
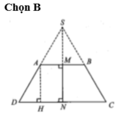
Gọi S là giao điểm của AD và BC. Nếu quay tam giác SCD quanh trục SN, các đoạn thẳng SC. SB lần lượt tạo ra mặt xung quanh của hình nón ( H 1 ) v à ( H 2 ) .
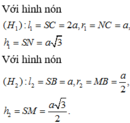
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Cho hình thang cân ABCD (AB // CD) có E, F lần lượt là trung điểm
của các đáy AB, CD. Chứng minh EF vuông góc với AB và CD.

Do ABCD là hình thang cân
\(\Rightarrow AD=BC\) và \(\widehat{FDA}=\widehat{FCB}\)
Do F là trung điểm của CD (gt)
\(\Rightarrow FC=FD\)
Xét \(\Delta ADF\) và \(\Delta BCF\) có:
\(AD=BC\) (cmt)
\(\widehat{FDA}=\widehat{FCB}\) (cmt)
\(FD=FC\) (cmt)
\(\Rightarrow\Delta ADF=\Delta BCF\) (c-g-c)
\(\Rightarrow AF=BF\) (hai cạnh tương ứng)
\(\Delta FAB\) có:
\(AF=BF\) (cmt)
\(\Rightarrow\Delta FAB\) cân tại F
Lại có E là trung điểm của AB
\(\Rightarrow FE\) là đường trung tuyến của \(\Delta FAB\)
\(\Rightarrow FE\) cũng là đường cao của \(\Delta FAB\)
\(\Rightarrow FE\perp AB\)
Mà AB // CD (gt)
\(\Rightarrow FE\perp CD\)
Vậy EF vuông góc với AB và CD
Trong không gian, cho hình thang cân ABCD có AB//CD, A B = a , C D = 2 a , A D = a . Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S φ của khối K.
A. S φ = 9 π a 2 4
B. S φ = 17 π a 2 4
C. S φ = 7 π a 2 4
D. S φ = 11 π a 2 4
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S t p của khối K.
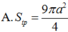
![]()