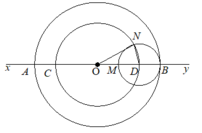
Trên đường thẳng xy lấy một điểm O. Vẽ đường tròn (O;3cm) cắt Ox, Oy theo thứ tự tại A, B. Vẽ đường tròn (O;2cm) cắt Ox, Oy theo thứ tự tại C, D. Vẽ đường tròn (D;DB) cắt BO tại M và cắt đường tròn (O;2cm) tại N. So sánh tổng ON+ND với OB.
PB
Những câu hỏi liên quan
Trên đường thẳng xy lấy một điểm O. Vẽ đường tròn (O;3cm) cắt Ox, Oy theo thứ tự tại A, B. Vẽ đường tròn (O;2cm) cắt Ox, Oy theo thứ tự tại C, D. Vẽ đường tròn (D;DB) cắt BO tại M và cắt đường tròn (O;2cm) tại N. Chứng tỏ rằng M là trung điểm của OD.
Trên đường thẳng xy lấy một điểm O. Vẽ đường tròn (O;3cm) cắt Ox, Oy theo thứ tự tại A, B. Vẽ đường tròn (O;2cm) cắt Ox, Oy theo thứ tự tại C, D. Vẽ đường tròn (D;DB) cắt BO tại M và cắt đường tròn (O;2cm) tại N. So sánh AC, BD.
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?

a)

b) Đoạn thẳng AB cắt đường thẳng xy
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và một điểm A cố định trên đường tròn đó. Qua A vẽ tiếp tuyến xy. Từ một điểm M trên xy vẽ tiếp tuyến MB với đường tròn (O). Hai đường cao AD và BE của tam giác MAB cắt nhau tại H.
a) Chứng minh rằng ba điểm M, H, O thẳng hàng.
b) Chứng minh rằng tứ giác AOBH là hình thoi.
c) Khi điểm M di động trên xy thì điểm H di động trên đường nào?
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
Suy ra: \(\widehat{MAB}=\widehat{MBA}\)
Xét ΔDAB vuông tại D và ΔEBA vuông tại E có
BA chung
\(\widehat{DBA}=\widehat{EAB}\)
Do đó: ΔDAB=ΔEBA
Suy ra: \(\widehat{DAB}=\widehat{EBA}\)
hay \(\widehat{HAB}=\widehat{HBA}\)
Xét ΔHBA có \(\widehat{HAB}=\widehat{HBA}\)
nên ΔHBA cân tại H
Suy ra: HA=HB
hay H nằm trên đường trung trực của AB(1)
Ta có:MA=MB
nên M nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,M thẳng hàng
Đúng 2
Bình luận (0)
Cho đường tròn tâm O đường kính AB và điểm H cố định trên AB , Từ B vẽ tiếp tuyến xy và trên xy lấy K di động. Vẽ đường tròn (K , KH) cắt đường tròn O tại C và D . Chứng minh rằng đường thẳng CD luôn đi qua 1 điêm cố định
Cho đường tròn (O; 2 cm) và một điểm A chạy trên đường tròn đó. Từ A vẽ tiếp tuyến xy. Trên xy lấy một điêm M sao cho AM = 2 3 cm. Hỏi điểm M di động trên đường nào khi A chạy trên (O)?
Tính được OM = 4 => M di chuyển trên (O;4cm)
Đúng 0
Bình luận (0)
cho đường tròn (O;2cm) và một điểm A chạy trên đường tròn đó .Từ A vẽ tiếp tuyến xy .Trên xy lấy một điểm M sao cho AM =2\(\sqrt[]{3}\) cm .Hỏi điểm M di động trên đường nào
trên đường thẳng xy lấy 1 điểm O. ẽ đường tròn (O;3cm) cắt Ox, Oy thứ tự tại A và B. VẼ đường tròn (0;2cm) cắt tia Ox, Oy thứ tự taijC và D. Vẽ đường tròn D; BD) cắt BO tại M và cắt đường tròn (O; 2cm) tại N
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
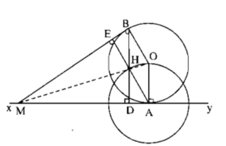
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Đúng 1
Bình luận (0)