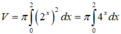Cho hình phẳng (H) giới hạn bởi các đường y = x 2 - x + 1 , y=0, x=0, x=2. Gọi V là thể tích khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào sau đây đúng?
A. 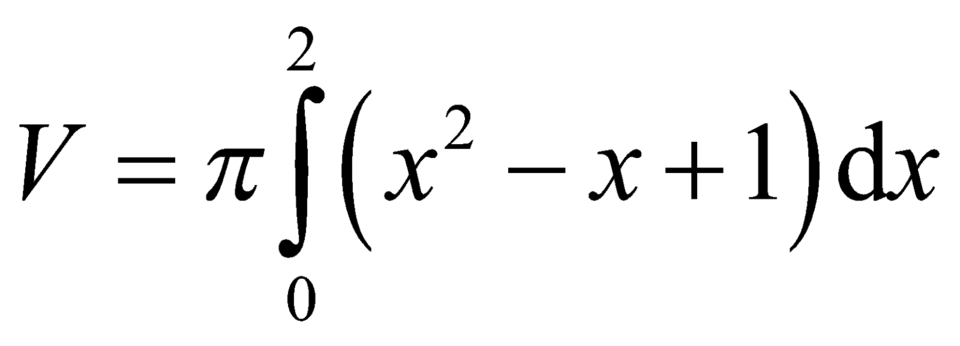
B. 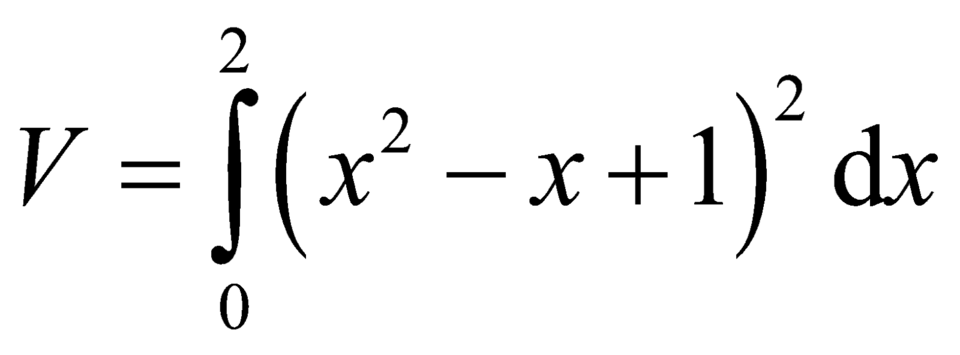
C. 
D. 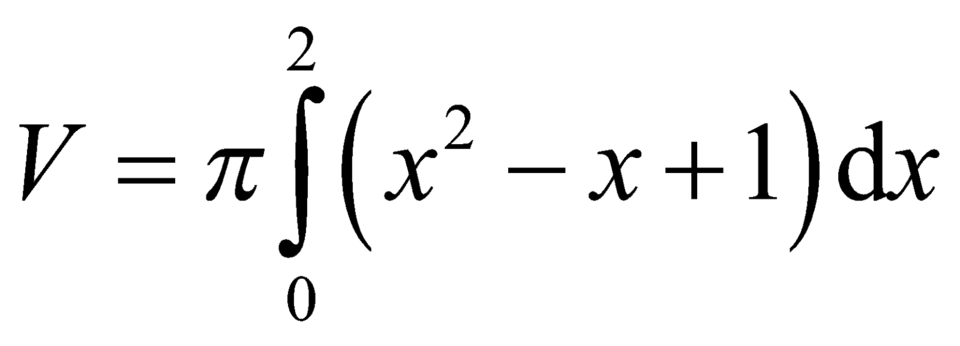
Cho hình phẳng (H) giới hạn bởi các đường y = x 2 + 3 ; y = 0 ; x = 0 ; x = 2 . Gọi V là thể tích khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox. Mệnh đề nào sau đây đúng?
A. V = π ∫ 0 2 x 2 + 3 2 d x
B. V = ∫ 0 2 x 2 + 3 d x
C. V = ∫ 0 2 x 2 + 3 2 d x
D. V = π ∫ 0 2 x 2 + 3 d x
Thể tích của khối tròn xoay tạo thành là:
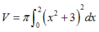
Chọn: A
Tính thể tích hình khối do hình phẳng giới hạn bởi các đường y=\(x^{\dfrac{1}{2}}e^{\dfrac{x}{2}}\) y=0,x=1,x=4
Tính thể tích hình khối do hình phẳng giới hạn bởi các đường y= \(x\sqrt{ln\left(1+x^3\right)}\) : y=0 : x=1
1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = e x , y = 0 , x = 0 , x = 2 Mệnh đề nào dưới đây đúng?
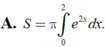
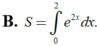
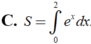
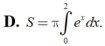
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 Mệnh đề nào dưới đây đúng?
A. S = π ∫ 0 2 l 2 x d x
B. S = ∫ 0 2 l 2 x d x
C. S = ∫ 0 2 l x d x
D. S = π ∫ 0 2 l x d x
Chọn C
Diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 được tính theo công thức S = ∫ 0 2 l x d x = ∫ 0 2 l x d x
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1/x, y=0, x=1, x=a, a>1. Tìm a để V = 2.
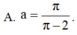
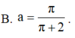
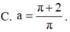
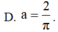
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Mệnh đề nào dưới đây đúng?
A. S = ∫ 0 2 3 x d x
B. S = π ∫ 0 2 3 2 x d x
C. S = π ∫ 0 2 3 x d x
D. ∫ 0 2 3 2 x d x
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1 x , y = 0 , x = 1 , x = a a > 1 . Tìm a để V = 2.
A. a = π π - 2
B. a = π π + 2
C. a = π + 2 π
D. a = 2 π
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y=1/x, y=0, x=a, a>1. Tìm a để V = 2.
A. a = π π - 2
B. a = π π + 2
C. a = π + 2 π
D. a = 2 π
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x
Đáp án D
Phương pháp:
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng x = a , x = b ( a < b ) và các đồ thị hàm số ư
y = f(x), y = g(x) khi quay quanh trục Ox là: V = π ∫ a b f 2 x - g 2 x dx
Cách giải:
Ta có công thức tính thể tích hình phẳng đã cho là: