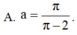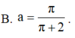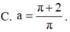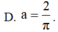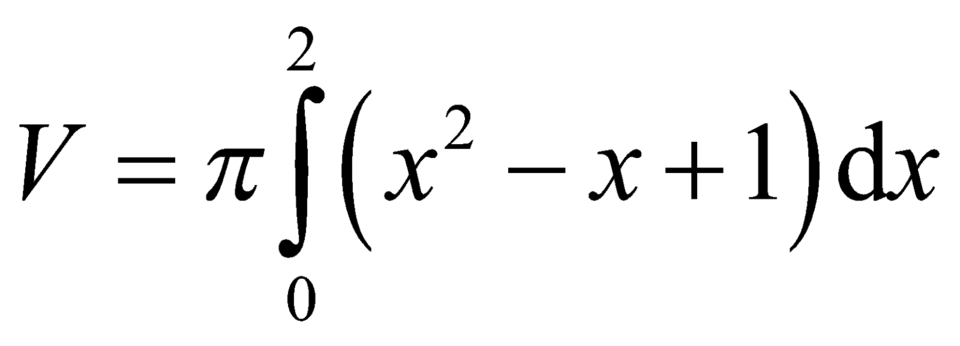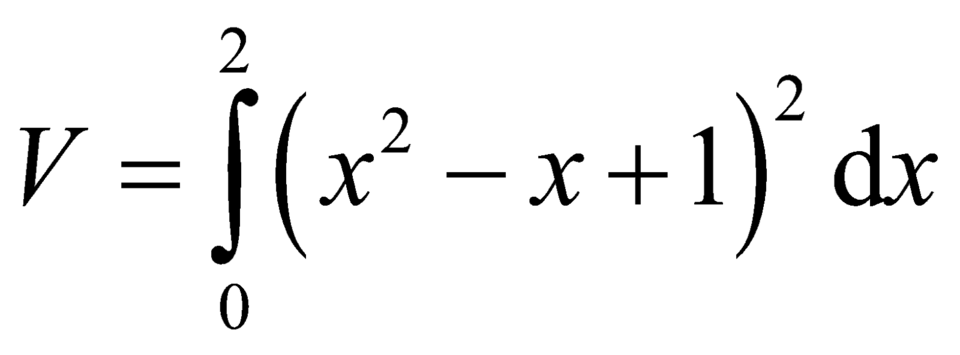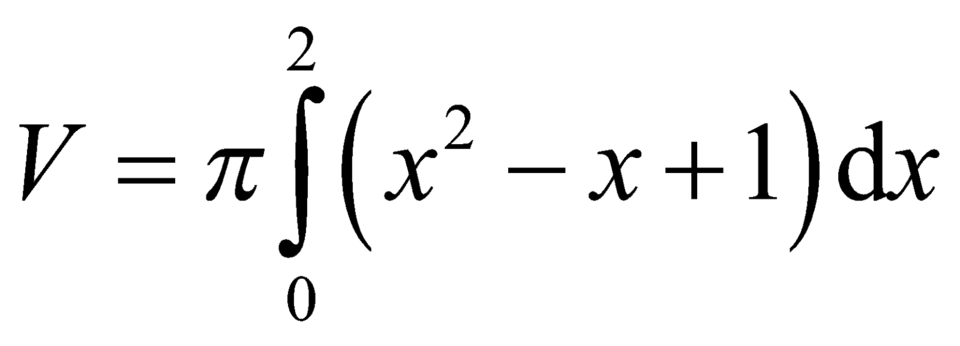Các câu hỏi tương tự
Cho hình phẳng (H) giới hạn bởi các đường y cos x, y0, x0, . Thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox bằng A. . B. . C. D. .
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y= cos x, y=0, x=0, ![]() . Thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox bằng
. Thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox bằng
A. ![]() .
.
B. ![]() .
.
C. ![]()
D. ![]() .
.
Cho hình phẳng (H) giới hạn bởi các đường
y
e
x
,
y
0
,
x
0
,
x
k
k
0
. Gọi
V
k
là thể tích khối tròn xoay khi quay hình (H) quanh trục Ox. Biết rằng
V
k
4
π...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y = e x , y = 0 , x = 0 , x = k k > 0 . Gọi V k là thể tích khối tròn xoay khi quay hình (H) quanh trục Ox. Biết rằng V k = 4 π . Kết luận nào sau đây là đúng?
A. 1 < k < 3 2 .
B. 3 2 < k < 2.
C. 1 2 < k < 1.
D. 0 < k < 1 2 .
Cho hình phẳng (D) được giới hạn bởi các đường x0, x1, y0 và
y
2
x
+
1
.Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0, x=1, y=0 và y = 2 x + 1 .Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
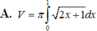
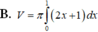
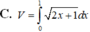
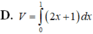
Cho hình phẳng (D) được giới hạn bởi các đường x 0; x 1; y 0 và
y
2
x
+
1
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0; x = 1; y = 0 và y = 2 x + 1 . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
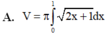
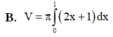
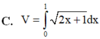
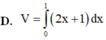
Gọi (D) là hình phẳng giới hạn bởi các đường
y
2
x
,
y
0
,
x
0
v
à
x
2
. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức: A.
V
π
∫
0
2...
Đọc tiếp
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y
x
,
y
0
và
x
4
quanh trục Ox. Đường thẳng x a (0 a 4 cắt đồ thị hàm số
y
x
tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V2V1. Khi đó A. . B. . C. . D. .
Đọc tiếp
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0< a< 4 cắt đồ thị hàm số y = x tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V=2V1. Khi đó
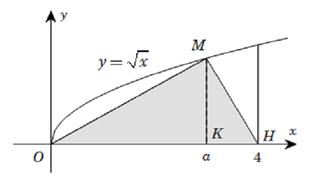
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y
xe
x
, y0, x0, x1 xung quanh trục Ox là: A. B. C. D.
Đọc tiếp
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = xe x , y=0, x=0, x=1 xung quanh trục Ox là:
A. 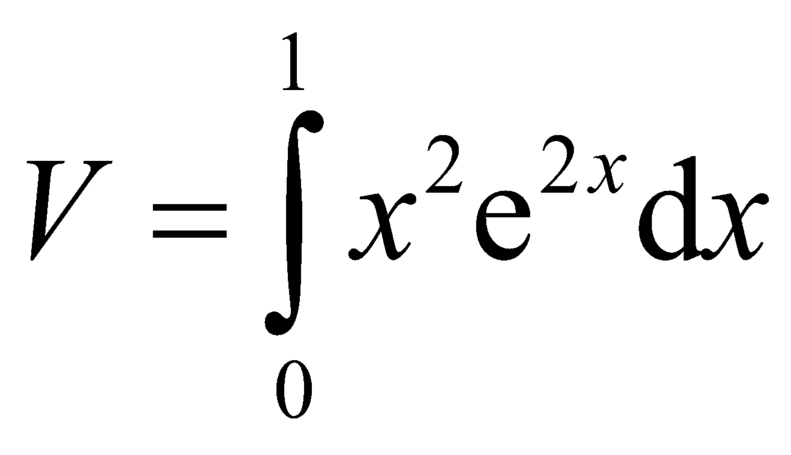
B. 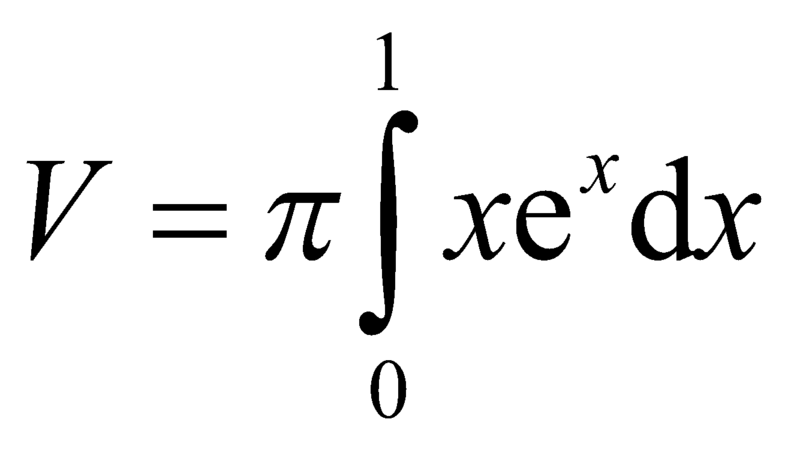
C. 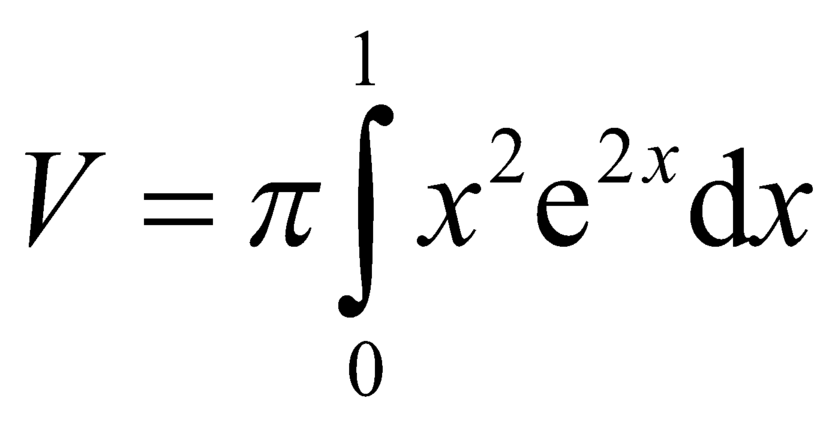
D. 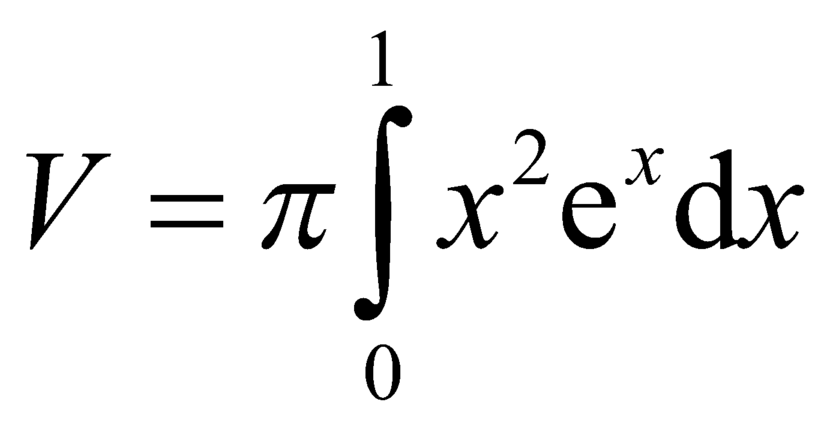
Cho hình phẳng (D) được giới hạn bởi các đường x0;
x
π
; y 0 và y -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0; x = π ; y = 0 và y = -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
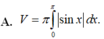
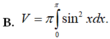
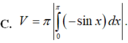
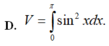
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y 1/x, y0, x1, xa, a1. Tìm a để V 2.
Đọc tiếp
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1/x, y=0, x=1, x=a, a>1. Tìm a để V = 2.