Hàm số y = x 4 + m x 2 − m − 5 (m là tham số) có 3 điểm cực trị khi các giá trị của m là
A. 4 < m < 5
B. m < 0
C. m > 8
D. m = 1
Cho hàm số y = (m − 2)x + 5 có đồ thị là đường thẳng (d) (m là tham số, 𝑚 ≠ 2) a) Vẽ đồ thị hàm số trên với 𝑚 = 4 b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 2. c) Tìm m để đồ thị cắt trục tung tại điểm có tung độ -3.
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
có đồ thị C và bảng biến thiên sau:
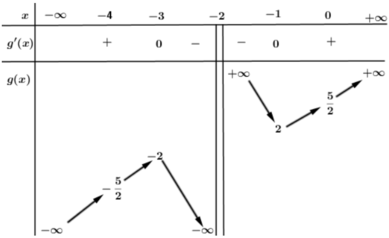
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 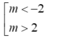
C. m < -5/2
D. m> 5 2
Xét phương trình f’ (x) = x2+(4-m) x+5-2m=0
⇔ x 2 + 4 x + 5 = m ( x + 2 ) ⇔ g ( x ) = x 2 + 4 x + 5 x + 2 = m
Ta có nghiệm của f’ (x)=0 cũng là hoành độ giao điểm của g(x)=m
Khi đó từ bảng biến thiên ta có YCBT khi m> 2.
Chọn A.
Câu 2: Cho hàm số y = ( 3m-1)x + m +2 . Tìm tham số m để đồ thị hàm số cắt trục tung tại điểm có tung độ là −3.
Câu 3: Cho hàm số y = 2mx-3m+2 . Tìm tham số m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 2
Câu 2:
Thay x=0 và y=-3 vào (d), ta được:
m+2=-3
hay m=-5
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\left|x^3-3x^2+m-4\right|\) có đúng 5 điểm cực trị là?
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Bài 2: Cho hàm số: y = (m + 5)x – m Xác định giá trị của tham số m để đồ thị hàm số: a) Cắt trục hoành tại điểm có hoành độ bằng 3 b) Cắt trục tung tại điểm có tung độ bằng -4
Cho hàm số y=(2m+3)x-2m+5 ( với m là tham số và m ≠-1,5) có đồ thị hàm số là đường thẳng (d)
a.tìm m để hàm số trên nghịch biến
b. tìm m để (d) song song với đường thẳng (d1):y=(3m-2)x+1
c.tìm m để (d) cắt đường thẳng (d2):y=3x-1 tại một điểm có tung độ bằng 5
d.tìm m để (d) ctaws trục Ox ,Oy tại 2 điểm A và B sao cho diện tích tam giác AOB bằng 1
a: Để hàm số y=(2m+3)x-2m+5 nghịch biến trên R thì 2m+3<0
=>2m<-3
=>\(m< -\dfrac{3}{2}\)
b: Để (d)//(d1) thì
\(\left\{{}\begin{matrix}2m+3=3m-2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-m=-5\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=5\\m\ne2\end{matrix}\right.\)
=>m=5
c: Thay y=5 vào y=3x-1, ta được:
3x-1=5
=>3x=6
=>x=6/3=2
Thay x=2 và y=5 vào (d), ta được:
\(2\left(2m+3\right)-2m+5=5\)
=>\(4m+6-2m+5=5\)
=>2m+11=5
=>2m=-6
=>m=-6/2=-3
d: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m+3\right)x-2m+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(2m+3\right)=2m-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{2m-5}{2m+3}\end{matrix}\right.\)
=>\(A\left(\dfrac{2m-5}{2m+3};0\right)\)
\(OA=\sqrt{\left(\dfrac{2m-5}{2m+3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{2m-5}{2m+3}\right)^2}=\left|\dfrac{2m-5}{2m+3}\right|\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x\left(2m+3\right)-2m+5=0\left(2m+3\right)-2m+5=-2m+5\end{matrix}\right.\)
=>\(B\left(-2m+5;0\right)\)
\(OB=\sqrt{\left(-2m+5-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-2m+5\right)^2}=\left|2m-5\right|\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot\left|2m-5\right|\cdot\dfrac{\left|2m-5\right|}{\left|2m+3\right|}\)
\(=\dfrac{1}{2}\cdot\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}\)
Để \(S_{AOB}=1\) thì \(\dfrac{\dfrac{1}{2}\left(2m-5\right)^2}{\left|2m+3\right|}=1\)
=>\(\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}=2\)
=>\(\left(2m-5\right)^2=2\left|2m+3\right|\)
=>\(\left(2m-5\right)^2=2\left(2m+3\right)\)
=>\(4m^2-20m+25-4m-6=0\)
=>\(4m^2-24m+19=0\)
=>\(m=\dfrac{6\pm\sqrt{17}}{2}\)
TÌM THAM SỐ MLÀ SỐ THỰC CỦA ĐỂ HÀM SỐ Y = 1/3X³ - MX² + (M² – 4)X + 3 ĐẠT CỰC ĐẠI TẠI X = 3. A. M = -7 B. M = 1 C. MTÌM THAM SỐ MLÀ SỐ THỰC CỦA ĐỂ HÀM SỐ Y = 1/3X³ - MX² + (M² – 4)X + 3 ĐẠT CỰC ĐẠI TẠI X = 3. A. M = -7 B. M = 1 C. M = -1 D. M = 5. = -1 D. M = 5.
Cho hàm số f ( x ) = m - 2 x 3 - 2 2 m - 3 x 2 + 5 m - 3 x - 2 m - 2 với m là tham số thực. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x có 5 điểm cực trị?
A. 0.
B. 3.
C. 2.
D. 1.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

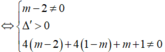
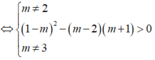
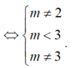

Chọn D