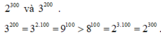So sánh: 2300 và 3200
PB
Những câu hỏi liên quan
so sánh A= -15/2300 + -17/3200
B=-17/2300 + -15/3200
So sánh: 2 300 và 3 200
Bài 1: So sánh
1/ a) 2300 và 3200 b) 9920 và 999910 c) 3500 và 7300
d) 202303 và 303202 e) 10750 và 7375
a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
Đúng 3
Bình luận (0)
\(\left(d\right):202^{303}=\left(202^3\right)^{101}=8242408^{101}>303^{202}=\left(303^2\right)^{101}=91809^{101}\)
\(\left(e\right):107^{50}=\left(107^2\right)^{25}=11449^{25}< 73^{75}=\left(73^3\right)^{25}=389017^{25}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
mk mới lập nick xin các bạn chỉ bảo cho
so sánh \(\frac{2017}{2300}\)và \(\frac{2016}{3200}\)
\(\frac{2017}{2300}\)lớn hơn\(\frac{2016}{3200}\)
chúc bạn học tốt !
Đúng 0
Bình luận (0)
\(\frac{2017}{2300}\)<\(\frac{2016}{2300}\)
Đúng 0
Bình luận (0)
a) 3200 và 2300 b) 27101 và 8135
c) 2332 và 3223
MN CHỈ E CÁCH SÓ SÁNH VS Ạ, E CẢM ƠN
`@` `\text {Ans}`
`\downarrow`
`a)`
\(3^{200}\text{ và }2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì `9 > 8 => 9^100 > 8^100`
`=> 3^200 > 2^300`
`b)`
\(27^{101}\text{ và }81^{35}\)
\(27^{101}=\left(3^3\right)^{101}=3^{303}\)
\(81^{35}=\left(3^4\right)^{35}=3^{140}\)
Vì `303 > 140 => 3^303 > 3^140`
`=> 27^101 > 81^35`
`c)`
\(2^{332}\text{ và }3^{223}\)
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì `9 > 8 => 9^111 > 8^111`
`=> 2^332 < 3^223.`
Đúng 3
Bình luận (0)
a: 3^200=9^100
2^300=8^100
mà 9>8
nên 3^200>2^300
b: 27^101=3^303
81^35=3^140
mà 303>140
nên 27^101>81^35
c: 2^332<2^333=8^111
3^223>3^222=9^111
mà 9>8
nên 3^223>8^111>2^332
Đúng 3
Bình luận (0)
So snhs các cặp số sau :
a. A = 275 và B = 2433
b. A = 2300 và B = 3200
1,Tìm x:
a,2x=16 b,x3=27 c,x50=x d,(x - 22)=16
2,So sánh:a,2300 và 3200
b,3500 và 7300
a) \(2^x=16=2^4\Rightarrow x=4\)
b) \(x^3=27=3^3\Rightarrow x=3\)
c) \(x^{50}=x\Rightarrow x\left(x^{49}-1\right)=0\Rightarrow x=0\) hay \(x=1\)
d) \(\left(x-2\right)^2=16=4^2\Rightarrow x-2=4\) hay \(x-2=-4\)
\(\Rightarrow x=6\) hay \(x=-2\)
Đúng 2
Bình luận (0)
a) \(2^{300}=2^{3.100}=8^{100}\)
\(3^{200}=3^{2.100}=9^{100}\)
vì \(8^{100}< 9^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(3^{500}=3^{5.100}=243^{100}\)
\(7^{300}=7^{3.100}=343^{100}\)
vì \(243^{100}< 343^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
Đúng 1
Bình luận (0)
`@` `\text {Ans}`
`\downarrow`
`1,`
`a,`
`2^x = 16`
`=> 2^x = 2^4`
`=> x = 4`
Vậy, `x = 4`
`b,`
`x^3 = 27`
`=> x^3 = 3^3`
`=> x = 3`
Vậy, `x = 3`
`c,`
\(x^{50}=x\)
`=>`\(x^{50}-x=0\)
`=>`\(x\left(x^{49}-1\right)=0\)
`=>`\(\left[{}\begin{matrix}x=0\\x^{49}-1=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=0\\x^{49}=1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy, `x \in {0; 1}`
`d,`
`(x-2^2)=16`
`=> x - 2^2 = 16`
`=> x = 16 + 2^2`
`=> x = 20`
Vậy, `x = 20`
`2,`
`a,`
Ta có:
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
Vì `8 < 9 =>`\(8^{100}< 9^{100}\)
`=>`\(2^{300}< 3^{200}\)
Vậy, \(2^{300}< 3^{200}\)
`b,`
Ta có:
\(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}\)
Vì `243 < 343 =>`\(243^{100}< 343^{100}\)
`=>`\(3^{500}< 7^{300}\)
Vậy, \(3^{500}< 7^{300}.\)
Đúng 0
Bình luận (0)
mk mới tạo nick mong các bn chỉ bảo
So sánh \(\frac{2017}{2300}\)và \(\frac{2016}{3200}\)
Các bn ghi cách giải từng bước cho mk nhé!!!!
Cảm ơn các bạn!!!>_<
\(\frac{2017}{2300}\)có mẫu số bé hơn \(\frac{2016}{3200}\)
\(=>\frac{2017}{2300}>\frac{2016}{3200}\)
Đúng 0
Bình luận (0)
Bài 2. So sánh.a . 2300 và 3200 b . 3500 và 7300c . 85 và 3 . 47 d . 202303 và 303202e. 9920 và 999910f.111979 và 371320g. 1010 và 48 . 505 h. 199010 + 19909 và 199110
Đọc tiếp
Bài 2. So sánh.
a . 2300 và 3200
b . 3500 và 7300
c . 85 và 3 . 47
d . 202303 và 303202
e. 9920 và 999910
f.111979 và 371320
g. 1010 và 48 . 505
h. 199010 + 19909 và 199110
a: \(2^{300}=8^{100}\)
\(3^{200}=9^{100}\)
mà 8<9
nên \(2^{300}< 3^{200}\)
b: \(3^{500}=243^{100}\)
\(7^{300}=343^{100}\)
mà 243<243
nên \(3^{500}< 7^{300}\)
Đúng 0
Bình luận (0)