Tổng tất cả các giá trị thực của m để hàm số y = 1 2 m 2 x 5 - 1 3 m x 3 + 10 x 2 - m 2 - m - 20 x + 1 đồng biến trên R bằng
A. 5 2
B. - 2
C. 1 2
D. 3 2
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2 3
C. 1.
D. 5.

![]()
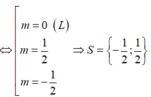
Vậy tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là 1.
Chọn C
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m 2 x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2/3
C. 1.
D. 5.
1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
Cho hàm số y = - x 3 + 4 x 2 + 1 có đồ thị (C) và điểm M(m ;1). Gọi S là tập hợp tất cả các giá trị thực của m để qua M kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tổng giá trị tất cả các phần tử của S bằng
A. 5
B. 40/9
C. 16/9
D. 20/3
Tổng tất cả các giá trị thực của m để hàm số y = 1 2 m 2 x 5 - 1 3 m x 3 + 10 x 2 - m 2 - m - 20 x + 1 đồng biến trên ℝ bằng
A. 5 2
B. -2
C. 1 2
D. 3 2
Có ![]()
![]()
ĐK cần: Để ý g(x)=0 có một nghiệm x=-1 do vậy g ( x ) ≥ 0 , ∀ x thì trước tiên g(x) không đổi dấu khi qua điểm x=-1 tức g(x)=0 có nghiệm kép
![]()


Điều kiện đủ: Bước tiếp theo cần thử lại:
+) Với
![]()
![]()
+) Với

![]()
Vậy ![]() là các giá trị cần tìm.
là các giá trị cần tìm.
Chọn đáp án C.
*Chú ý bước thử lại các em nên dùng máy CASIO 580 hoặc VINACAL 570 EXPLUS giải bất phương trình bậc bốn để kiểm tra cho nhanh.
Tổng tất cả các giá trị thực của m để hàm số y = 1 5 m 2 x 5 - 1 3 m x 3 + 10 x 2 - m 2 - m - 20 x + 1 đồng biến trên R bằng

![]()


1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !