Có bao nhiêu nghiệm nguyên thuộc khoảng (-9;9) của tham số m để bất phương trình sau có nghiệm thực: 3 logx ≤ 2 log m x - x 2 - ( 1 - x ) 1 - x ?
A. 6.
B. 7.
C. 10.
D. 11.
Có bao nhiêu số nguyên m để phương trình 4x - m.2x+1 + 9 = 0 có đúng một nghiệm thuộc khoảng (0;2)
\(2^x=t\Rightarrow t\in\left(1;4\right)\)
\(t^2-2m.t+9=0\)
\(\Leftrightarrow m=\dfrac{t^2+9}{2t}\)
Xét \(f\left(t\right)=\dfrac{t^2+9}{2t}\) trên (1;4),
\(f\left(1\right)=5\) ; \(f\left(4\right)=\dfrac{25}{8}\) ; \(f\left(t\right)=\dfrac{t^2+9}{2t}\ge\dfrac{6t}{2t}=3\)
\(\Rightarrow f\left(t\right)\) có 2 nghiệm khi \(3< m< \dfrac{25}{8}\) và có 1 nghiệm khi \(\dfrac{25}{8}\le m< 5\)
Có 1 giá trị m
Chà câu kia mỏi cổ quá:
Nhân 2 vế với \(3^{6\sqrt{x}-1}\) và rút gọn:
\(3^{\dfrac{3}{x}+6\sqrt{x}}-3.3^{\dfrac{2}{x}+2\sqrt{x}}+\left(m+2\right)3^{\dfrac{1}{x}+2\sqrt{x}}-m=0\)
\(\Leftrightarrow\left(3^{\dfrac{1}{x}+2\sqrt{x}}\right)^3-3.\left(3^{\dfrac{1}{x}+2\sqrt{x}}\right)^2+\left(m+2\right).3^{\dfrac{1}{x}+2\sqrt{x}}-m=0\)
\(\dfrac{1}{x}+2\sqrt{x}=\dfrac{1}{x}+\sqrt{x}+\sqrt{x}\ge3\sqrt[3]{\dfrac{x}{x}}=3\)
Do đó đặt \(3^{\dfrac{1}{x}+2\sqrt{x}}=t\Rightarrow t\ge3^3=27\)
\(\Rightarrow t^3-3t^2+\left(m+2\right)t-m=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2-2t+m\right)=0\)
\(\Leftrightarrow t^2-2t+m=0\)
\(\Leftrightarrow m=-t^2+2t\)
Xét hàm \(f\left(t\right)=-t^2+2t\) với \(t\ge27\), từ BBT dễ dàng suy ra \(m\le f\left(27\right)=-675\)
Có bao nhiêu giá trị nguyên thuộc khoảng (-9; 9) của tham số m để bất phương trình 3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x
có nghiệm thực?
A. 6
B. 7
C. 10
D. 11
Đáp án B.
Phương pháp:
Bất phương trình m ≥ f x , x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .
Cách giải:
ĐKXĐ: 0 < x < 1
3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x
⇔ m ≥ x x + 1 − x 1 − x x − x 2 , x ∈ 0 ; 1
Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2
Xét
f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1
Đặt t = x + 1 − x , t ∈ 1 ; 2
Khi đó,
f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t
g ' t = − t 4 − 3 t 2 − 1 2 < 0 , ∀ t ∈ 1 ; 2
⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2
Mà
m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒
Có 7 giá trị thỏa mãn.
Bất phương trình 3 x 2 + 3 . 2 x ≤ x . 2 x + 1 - 1 có bao nhiêu nghiệm nguyên thuộc khoảng(-10;10)?
A. 11.
B. 12.
C. 7.
D. 8.
Có bao nhiêu giá trị nguyên của a để phương trình cos 3 2 x − cos 2 2 x − a sin 2 x = 0 có nghiệm thuộc khoảng 0 ; π 6 .
A. 0
B. 1
C. 2
D. 3
Có nhiều nhất bao nhiêu số nguyên m thuộc nửa khoảng − 2017 ; 2017 để phương trình 2 x 2 − x − 2 m = x − 2 có nghiệm:
A. 2014
B. 2021
C. 2013
D. 2020
Phương trình đã cho tương đương với: x ≥ 2 2 x 2 − x − 2 m = x 2 − 4 x + 4 ⇔ x ≥ 2 x 2 + 3 x − 4 = 2 m
Xét hàm y = x 2 + 3 x − 4 trên 2 ; + ∞ ta có
BBT:
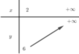
Để phương trình đã cho có nghiệm điều kiện là 2 m ≥ 6 ⇔ m ≥ 3
Mà m ∈ [ - 2017 ; 2017 ) suy ra 3 ≤ m < 2017
Vậy có nhiều nhất 2014 số nguyên thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: A
Bất phương trình \(x^2-2\left|x-1\right|+2>0\) có bao nhiêu nghiệm nguyên thuộc khoảng (-20; 30)
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3 x - cos 2 x + m cos x = 1 có đúng 7 nghiệm khác nhau thuộc khoảng - π 2 ; 2 π
A. 2.
B. 4.
C. không tồn tại.
D. 1.
Có bao nhiêu giá trị nguyên của m để phương trình e 3 x - 2 e 2 x + ln 3 + e x + ln 9 + m = 0 có 3 nghiệm phân biệt thuộc khoảng - ln 2 ; + ∞
A. 0.
B. 3.
C. 2
D. 1
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3 x - cos 2 x + m cos x = 1 có đúng bảy nghiệm khác nhau thuộc khoảng - π 2 ; 2 π
A. 3
B. 5
C. 7
D. 1